
| 县名 费用 仓库 | A | B |
| 甲 | 40 | 80 |
| 乙 | 30 | 50 |


科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 4 |
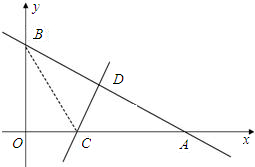
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
| 甲 | 3 | 1 | 12500 |
| 乙 | 2 | 3 | 16500 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
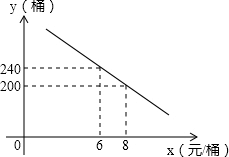 费用是a元.
费用是a元.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
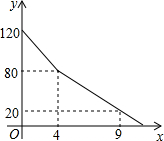 手中持有的钱数y(元)与购买糖果的数量x(千克)之间的函数关系如下图所示,请结合图象,回答下列问题:
手中持有的钱数y(元)与购买糖果的数量x(千克)之间的函数关系如下图所示,请结合图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 2x | 200 | |
| 运费(元) | 30x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com