
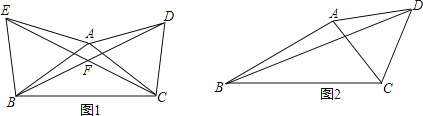
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;
(2)如图2,∠ABC=α,∠ACD=β,BC=4,BD=6.
①若α=30°,β=60°,AB的长为 ;
②若改变α、β的大小,且α+β=90°,求△ABC的面积.
【答案】(1)∠BFC=120°;(2)①2![]() ;(3)S△ABC=
;(3)S△ABC=![]() BCAH=2
BCAH=2![]() .
.
【解析】
(1)根据SAS,可首先证明△AEC≌△ABD,再利用全等三角形的性质,可得对应角相等,根据三角形的外角的定理,可求出∠BFC的度数;
(2)①在△ABC外作等边△BAE,连接CE,证明△EAC≌△BAD,可证∠EBC=90°,EC=BD=6,在Rt△BCE中,由勾股定理求BE即可;
②过点B作BE∥AH,并在BE上取BE=2AH,连接EA,EC.并取BE的中点K,连接AK,证明△EAC≌△BAD,求得EC=DB,利用勾股定理即可得出结论.
(1)∵∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠BAC,
∴∠EAC=∠DAB,
在△AEC和△ABD中,
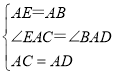 ,
,
∴△AEC≌△ABD(SAS),
∴∠AEC=∠ABD,
∵∠BFC=∠BEF+∠EBF=∠AEB+∠ABE,
∴∠BFC=∠AEB+∠ABE=120°;
(2)①如图2,以AB为边在△ABC外作正三角形ABE,连接CE.
由(1)可知△EAC≌△BAD.
∴EC=BD.
∴EC=BD=6,
∵∠BAE=60°,∠ABC=30°,
∴∠EBC=90°.
在Rt△EBC中,EC=6,BC=4,
∴EB= ![]() ,
,
∴AB=BE=![]() ;
;
故答案为:![]() .
.
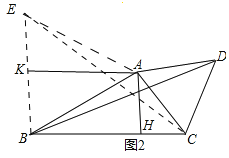
②如图2,作AH⊥BC交BC于H,过点B作BE∥AH,并在BE上取BE=2AH,连接EA,EC.并取BE的中点K,连接AK.
∵AH⊥BC于H,
∴∠AHC=90°.
∵K为BE的中点,BE=2AH,
∴BK=AH.
∵BK∥AH,
∴四边形AKBH为平行四边形.
又∵∠AHC=90°,
∴四边形AKBH为矩形.
∴∠AKB=90°,∠ABE=∠ACD,
∴AK是BE的垂直平分线.
∴AB=AE.
∵AB=AE,AC=AD,∠ABE=∠ACD,
∴∠EAB=∠DAC,
∴∠EAB+∠BAC=∠DAC+∠BAC,
即∠EAC=∠BAD,
在△EAC与△BAD中,
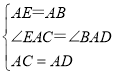
∴△EAC≌△BAD(SAS).
∴EC=BD=6.
在Rt△BCE中,BE=![]() ,
,
∴AH=![]() BE=
BE=![]() ,
,
∴S△ABC=![]() BCAH=2
BCAH=2![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x,0)且﹣2<x<3,BC⊥AC垂足为点C,连接AB.若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
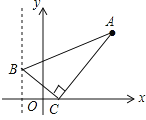
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
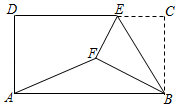
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
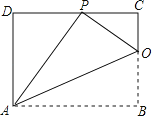
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=![]() ,求CP的长.
,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的
,求一个一元二次方程,使它的根分别是已知方程根的![]() 倍
倍
解:设所求方程的根为![]() ,则
,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]() .
.
化简,得![]()
故所求方程为![]() .
.
这种利用方程的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:_______________.
,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:_______________.
(2)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的倒数.
,求一个一元二次方程,使它的根分别是已知方程根的倒数.
(3)已知关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() )的两个实数根分别为
)的两个实数根分别为![]() ,
,![]() ,求一元二次方程
,求一元二次方程![]() 的两根.(直接写出结果)
的两根.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn的面积为Sn,则Sn= .(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=15,AD=20,P是AD边上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E,F,则PEPF的最大值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com