
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.
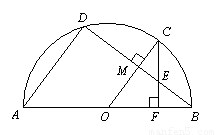
(1)求⊙O的半径;
(2)求证:CE=BE.
(1)5;(2)证明见解析.
【解析】
试题分析:(1)可在Rt△OBM中,用半径表示出OM,然后根据勾股定理求出半径的长;(2)由AAS证得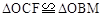 ,由等量减等量差相等得
,由等量减等量差相等得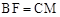 ,从而由AAS或ASA可证得
,从而由AAS或ASA可证得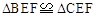 ,因此CE = BE
,因此CE = BE
试题解析:(1)∵AB为直径,∴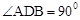 .
.
∵OC⊥BD,∴M为BD的中点.
∵BD=8,∴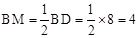 .
.
设半径为r,则OM=OC-CM=r-2,
∴在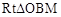 中,
中,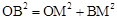 ,即
,即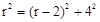 ,解得
,解得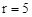 .
.
∴⊙O的半径为5.
(2)在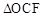 和
和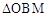 中,∵∠COF=∠BOM(公共角),∠CFO=∠BMO=90°,OC=OM1
中,∵∠COF=∠BOM(公共角),∠CFO=∠BMO=90°,OC=OM1
∴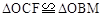 (AAS), ∴OF=OM.
(AAS), ∴OF=OM.
又OB=OC,∴ ,即
,即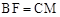 .
.
∴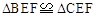 (AAS或ASA). ∴CE = BE.
(AAS或ASA). ∴CE = BE.
考点:1.圆周角定理;2.勾股定理;3.垂径定理;4.全等三角形的判定和性质.


科目:初中数学 来源: 题型:
 BD于点E,BD=8,CM=2.
BD于点E,BD=8,CM=2.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点A,B分别在x轴和y轴上,且OA=OB=3
如图,已知点A,B分别在x轴和y轴上,且OA=OB=3| 2 |
| 7 |
| 2 |
| 2 |
| 7 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com