
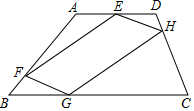
 如图,四边形ABCD中,点E、F、G、H分别在边AD、AB、BC、DC上,且$\frac{ED}{AE}$=$\frac{BF}{AF}$=$\frac{BG}{GC}$=+$\frac{DH}{CH}$=$\frac{1}{2}$
如图,四边形ABCD中,点E、F、G、H分别在边AD、AB、BC、DC上,且$\frac{ED}{AE}$=$\frac{BF}{AF}$=$\frac{BG}{GC}$=+$\frac{DH}{CH}$=$\frac{1}{2}$分析 (1)根据已知条件得到$\frac{DE}{AD}=\frac{DH}{DC}$=$\frac{1}{3}$根据相似三角形的判定和性质得到$\frac{EH}{AC}$=$\frac{DH}{DC}$=$\frac{1}{3}$,于是得到EH∥AC,同理:EH∥FG,根据平行四边形的判定定理即可得到结论;
(2)连接AC,BD,由(1)知,EH∥AC,$\frac{EH}{AC}$=$\frac{1}{3}$,求得EH=$\frac{1}{2}$AC得到EH=$\frac{2}{3}$BD,同理得到EF=$\frac{2}{3}$BD于是得到结论.
解答 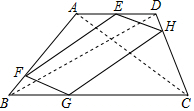 (1)证明:∵$\frac{ED}{AE}$=$\frac{DH}{CH}$=$\frac{1}{2}$,
(1)证明:∵$\frac{ED}{AE}$=$\frac{DH}{CH}$=$\frac{1}{2}$,
∴$\frac{DE}{AD}=\frac{DH}{DC}$=$\frac{1}{3}$,
∵∠D=∠D,
∴△ADC∽△EDH,
∴$\frac{EH}{AC}$=$\frac{DH}{DC}$=$\frac{1}{3}$,
∴EH∥AC,
同理:FG∥AC,$\frac{FG}{AC}$=$\frac{1}{3}$,
∴EH∥FG,$\frac{EH}{AC}$=$\frac{FG}{AC}$,
∴EH=FG,
∴四边形EFGH为平行四边形;
(2)解:当AC=2BD时,四边形EFGH为菱形,
理由:连接AC,BD,
由(1)知,EH∥AC,$\frac{EH}{AC}$=$\frac{1}{3}$,
∴EH=$\frac{1}{2}$AC,
∵AC=2BD,
∴EH=$\frac{2}{3}$BD,
同理,$\frac{EF}{BD}=\frac{2}{3}$,
∴EF=$\frac{2}{3}$BD,
∴EH=EF,
∴四边形EFGH为菱形.
点评 本题考查了相似三角形的判定和性质,平行线的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
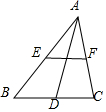 如图,在△ABC中,D、E、F分别是边BC、AB、AC的中点.
如图,在△ABC中,D、E、F分别是边BC、AB、AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
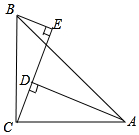 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$+$\sqrt{5}$ | B. | 2$\sqrt{3}$+2$\sqrt{5}$ | C. | 3$\sqrt{3}$+2$\sqrt{5}$ | D. | 3$\sqrt{3}$+$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里•吨),铁路运价为1元/(公里•吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.
如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里•吨),铁路运价为1元/(公里•吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 由于近年来电力紧缺,某省电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
由于近年来电力紧缺,某省电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
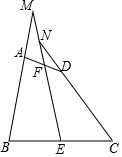 如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com