
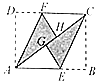
【题目】如图,在矩形纸片![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,把
上,把![]() 沿
沿![]() 翻折,
翻折,![]() 的落点是对角线
的落点是对角线![]() 上的点
上的点![]() 和
和![]() ,则四边形
,则四边形![]() 的面积是____________.
的面积是____________.
【答案】7.5
【解析】
直接根据矩形性质及平行四边形的判定证得四边形AECF是平行四边形,再根据勾股定理求出FC的长,最后利用平行四边形的面积公式计算即可得出结论.
解:∵翻折,
∴∠FAH=![]() ∠DAC,∠ECG=
∠DAC,∠ECG=![]() ∠BCA,
∠BCA,
∵四边形ABCD为矩形,
∴AD∥BC,AB∥CD,∠B=∠D=90°,
∴∠DAC=∠BCA,
∴∠FAH=∠ECG,
∴AF∥CE,
又∵AE∥CF,
∴四边形AECF是平行四边形,
∵在矩形纸片ABCD中,∠B=90°,AB=4,BC=3,
∴![]() ,
,
∵翻折,
∴∠FHA=∠D=90°,AH=AD=3,
同理可得,CG=3,
∴CH=AC-AH=5-3=2,
设DF=FH=x,则FC=4-x,
∵在Rt△FHC中,FC2=FH2+CH2,
∴(4-x)2=x2+22,
解得x=1.5,
∴FC=4-x=2.5,
∴四边形AECF的面积为FC·AD=2.5×3=7.5,
故答案为:7.5.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
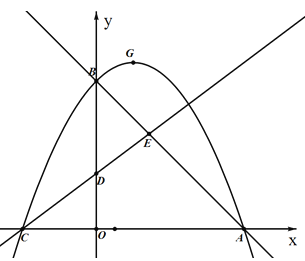
【题目】如图,在平面直角坐标系中,抛物线试纸y=ax2+bx+c与x轴交于点A,C,与y轴交于点B.已知点A坐标为(8,0),点B为(0,8),点D为(0,3),tan∠DCO=![]() ,直线AB和直线CD相交于点E.
,直线AB和直线CD相交于点E.
⑴ 求抛物线的解析式,并化成y=a(x-m)2+h的形式;
⑵ 设抛物线的顶点为G,请在直线AB上方的抛物线上求点P的坐标,使得S△ABP=S△ABG.
⑶ 点M为直线AB上的一点,过点M作x轴的平行线分别交直线AB,CD于点M,N,连结DM,DN,是否存在点M,使得△DMN为等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
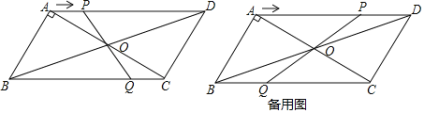
【题目】如图,在□ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)当t=3时四边形OQCD的面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.
(1)如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.
(2)一年中进入该公园超过多少次时,A类年票比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
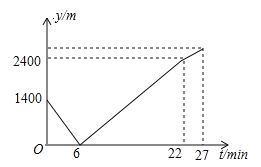
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
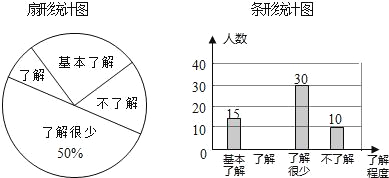
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:

(1)请估计:当![]() 很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率
很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率![]() .
.
(2)试估算盒子里白、黑两种颜色的球各有多少只?
(3)在(2)条件下如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
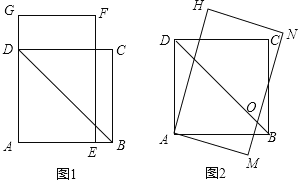
【题目】如图1,四边形ABCD是边长为![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
(1)求∠DOM的度数;
(2)图2中,求D、N两点间的距离;
(3)若将矩形AMNH绕点A再顺时针旋转15°得到矩形APQR,此时点B在矩形APQR的内部、外部还是边上?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com