练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（　　）

    A.84
    B.336
    C.510
    D.1326

    【答案】C
    【解析】解：1×73+3×72+2×7+6=510，
    故选C．
    类比于现在我们的十进制“满十进一”，可以表示满七进一的数为：千位上的数×73+百位上的数×72+十位上的数×7+个位上的数．本题是以古代“结绳计数”为背景，按满七进一计算自孩子出生后的天数，运用了类比的方法，根据图中的数学列式计算；本题题型新颖，一方面让学生了解了古代的数学知识，另一方面也考查了学生的思维能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（　　）

    A.
    B.2
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．
    （1）甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；
    （2）若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了落实省新课改精神，我是各校都开设了“知识拓展类”、“体艺特长类”、“实践活动类”三类拓展性课程，某校为了解在周二第六节开设的“体艺特长类”中各门课程学生的参与情况，随机调查了部分学生作为样本进行统计，绘制了如图所示的统计图（部分信息未给出）
    根据图中信息，解答下列问题：
    （1）求被调查学生的总人数；
    （2）若该校有200名学生参加了“体艺特长类”中的各门课程，请估计参加棋类的学生人数；
    （3）根据调查结果，请你给学校提一条合理化建议．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班10名学生的校服尺寸与对应人数如表所示：

    尺寸（cm）

    160

    165

    170

    175

    180

    学生人数（人）

    1

    3

    2

    2

    2

    则这10名学生校服尺寸的众数和中位数分别为（ ）
    A.165cm，165cm
    B.165cm，170cm
    C.170cm，165cm
    D.170cm，170cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为增强学生体质，各学校普遍开展了阳光体育活动，某校为了解全校1000名学生每周课外体育活动时间的情况，随机调查了其中的50名学生，对这50名学生每周课外体育活动时间x（单位：小时）进行了统计．根据所得数据绘制了一幅不完整的统计图，并知道每周课外体育活动时间在6≤x＜8小时的学生人数占24%．根据以上信息及统计图解答下列问题：

    （1）本次调查属于调查，样本容量是；
    （2）请补全频数分布直方图中空缺的部分；
    （3）求这50名学生每周课外体育活动时间的平均数；
    （4）估计全校学生每周课外体育活动时间不少于6小时的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

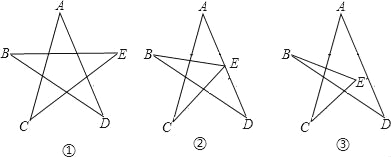
    【题目】如图①所示，为五角星图案，图②、图③叫做蜕变的五角星．试回答以下问

    （1）在图①中，试证明∠A+∠B+∠C+∠D+∠E=180°；

    （2）对于图②或图③，还能得到同样的结论吗？若能，请在图②或图③中任选其一证明你的发现；若不能，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（探究）如图①，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P．

    （1）若∠ABC=50°，∠ACB=80°，则∠A=　 　度，∠P=　 　度

    （2）∠A与∠P的数量关系为　 　，并说明理由．

    （应用）如图②，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P．∠ABC的外角平分线与∠ACB的外角平分线相交于点Q．直接写出∠A与∠Q的数量关系为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小明在教学楼上的窗口A看地面上的B、C两个花坛，测得俯角∠EAB=30°，俯角∠EAC=45°．已知教学楼基点D与点C、B在同一条直线上，且B、C两花坛之间的距离为6m．求窗口A到地面的高度AD．（结果保留根号）

    查看答案和解析>>

    同步练习册答案