
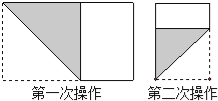
【题目】长为30,宽为a的矩形纸片(15<a<30),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n次操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为 .
【答案】18或22.5.
【解析】试题分析:根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽.当15<a<30时,矩形的长为30,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为30﹣a,a.由30﹣a<a可知,第二次操作时所得正方形的边长为30﹣a,剩下的矩形相邻的两边分别为30﹣a,a﹣(30﹣a)=2a﹣30.由于(30﹣a)﹣(2a﹣30)=60﹣3a,所以(30﹣a)与(2a﹣30)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①30﹣a>2a﹣30;②30﹣a<2a﹣30.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
解:由题意,可知当15<a<30时,第一次操作后剩下的矩形的长为a,宽为30﹣a,所以第二次操作时正方形的边长为30﹣a,第二次操作以后剩下的矩形的两边分别为30﹣a,2a﹣30.此时,分两种情况:
①如果30﹣a>2a﹣30,即a<20,那么第三次操作时正方形的边长为2a﹣30.
∵经过第三次操作后所得的矩形是正方形,
∴矩形的宽等于30﹣a,
即2a﹣30=(30﹣a)﹣(2a﹣30),解得a=18;
②如果30﹣a<2a﹣30,即a>20,那么第三次操作时正方形的边长为30﹣a.
则30﹣a=(2a﹣30)﹣(30﹣a),解得a=22.5.
故答案为:18或22.5.


科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.

(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)当BC为多长时,长方形面积达300m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
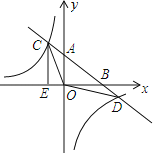
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积;
(3)直接写出使一次函数值小于反比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
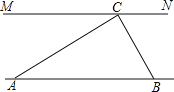
【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC内接于圆O,AB=AC,AB的垂直平分线MN与边AB交于点M,与AC所在的直线交于点N,若∠ANM=70°,则劣弧![]() 所对的圆心角的度数为 .
所对的圆心角的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com