
【题目】把一边长为36cm的正方形硬纸板进行适当的剪裁,折成一个长方体盒子(纸板的厚度忽略不计)
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.
①要使折成的长方体盒子的底面积为676cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子,若折成的一个长方体盒子的表面积为880cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况)

【答案】(1)①剪掉的正方形的边长为5cm, ②当剪掉的正方形的边长为9cm时,长方形盒子的侧面积最大为648cm2;(2)剪掉的正方形的边长为8cm.此时长方体盒子的长为20cm,宽为10cm,高为8cm.
【解析】分析:(1)①设剪掉的正方形的边长为xcm,根据题意得出(36-2x)2=676,求出即可;
②设剪掉的正方形的边长为xcm,盒子的侧面积为Scm2,则y与x的函数关系为:S=4(36-2x)x,利用二次函数最值求出即可;
(2)设剪掉的长方形盒子的高为acm,利用折成的一个长方形盒子的表面积为880cm2,得出等式方程求出即可.
详解:(1)①设剪掉的正方形的边长为xcm.
则(36﹣2x)2=676,即36﹣2x=±26,
解得:x1=31(不合题意,舍去),x2=5,
∴剪掉的正方形的边长为5cm.
②侧面积有最大值.设剪掉的正方形的边长为xcm,盒子的侧面积为Scm2,
则S与x的函数关系为:
S=(36﹣2x)×x×4=﹣8x2+144x=﹣(x﹣9)2+648,
∴x=9时,S最大=648.
即当剪掉的正方形的边长为9cm时,长方形盒子的侧面积最大为648cm2;
(2)在如图的一种剪裁图中,

设剪掉的正方形的边长为acm,长为(36﹣2a)cm,宽为(18﹣a)cm,高为acm.
(36﹣2a)×36+2a(18﹣a)=880
解得:a1=﹣26(不合题意,舍去),a2=8.
∴剪掉的正方形的边长为8cm.此时长方体盒子的长为20cm,宽为10cm,高为8cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,已知甲工程队铺设每天需支付工程费2000元,乙工程队铺设每天需支付工程费1500元.
(1)甲、乙两队合作施工多少天能完成该管线的铺设?
(2)由两队合作完成该管线铺设工程共需支付工程费多少元?
(3)根据实际情况,若该工程要求10天完成,从节约资金的角度应怎样安排施工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )

A. AB B. BC C. AC D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=﹣![]() x+1,直线AC交x轴于点C,交y轴于点A.
x+1,直线AC交x轴于点C,交y轴于点A.
(1)若等边△OBD的顶点D与点C重合,另一顶点B在第一象限内,直接写出点B的坐标;
(2)过点B作x轴的垂线l,在l上是否存在一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)试在直线AC上求出到两坐标轴距离相等的所有点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.
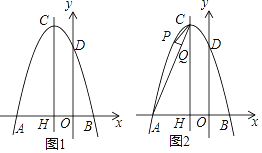
(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() (0,5),与直线
(0,5),与直线![]() 交于点
交于点![]() (﹣1,
(﹣1,![]() ),且与
),且与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)求△![]() 的面积.
的面积.
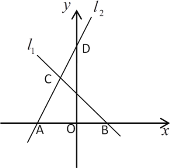
查看答案和解析>>
科目:初中数学 来源: 题型:
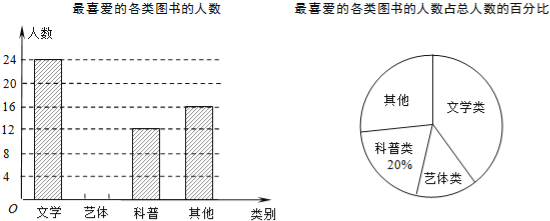
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com