
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
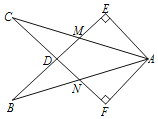
【题目】如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在坐标平面内,等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
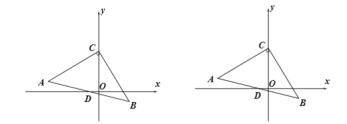
(1)求点![]() 的坐标;
的坐标;
(2)求点![]() 的坐标;
的坐标;
(3)如图,点![]() 在
在![]() 轴上,当
轴上,当![]() 的周长最小时,求出点
的周长最小时,求出点![]() 的坐标;
的坐标;
(4)在直线![]() 上有点
上有点![]() ,在
,在![]() 轴上有点
轴上有点![]() ,求出
,求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面方法,解答后面的问题:
(阅读理解)我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用。
例题:已知x可取任意实数,试求二次三项式![]() 的取值范围。
的取值范围。
解: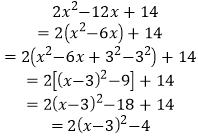
∵x取任何实数,总有![]() ,∴
,∴![]() 。
。
因此,无论x取任何实数,![]() 的值总是不小于-4的实数。
的值总是不小于-4的实数。
特别的,当x=3时,![]() 有最小值-4
有最小值-4
(应用1):已知x可取任何实数,则二次三项式![]() 的最值情况是( )
的最值情况是( )
A. 有最大值-10 B. 有最小值-10 C. 有最大值-7 D. 有最小值-7
(应用2):某品牌服装进货价为每件50元,商家在销售中发现:当以每件90元销售时,平均每天可售出20件,为了扩大销售量,增加盈利,商家决定采取适当的降价措施。
(1)将市场调查发现:如果每件服装降价1元,那么平均每天那就可多售出2件,要想平均每天销售这种服装盈利为1200元,我们设降价x元,根据题意列方程得( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
(2)请利用上面(阅读理解)提供的方法解决下面问题:
这家服装专柜为了获得每天的最大盈利,每件服装需要降价多少元?每天的最大盈利又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
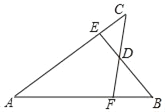
A. ① B. ② C. ①和② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路![]() 的一侧点
的一侧点![]() 处有一村庄,村庄
处有一村庄,村庄![]() 到公路
到公路![]() 的距离为800米,假使宣讲车
的距离为800米,假使宣讲车![]() 周围1000米以内能听到广播宣传,宣讲车
周围1000米以内能听到广播宣传,宣讲车![]() 在公路
在公路![]() 上沿
上沿![]() 方向行驶时:
方向行驶时:

(1)请问村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
查看答案和解析>>
科目:初中数学 来源: 题型:
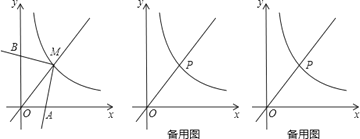
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(1)求k的值;
(2)点P在反比例函数y=![]() (x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
(x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
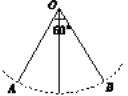
【题目】如图所示,秋千链子的长度为4 m,当秋千向两边摆动时,两边的最大摆动角度均为30°.则它摆动至最高位置与最低位置的高度之差为( )
A. 2 m B. (4-![]() ) m C. (4-2
) m C. (4-2![]() ) m D. (4-2
) m D. (4-2![]() ) m
) m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com