
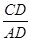 =
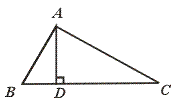
=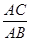 ; (4)AB2=BD·BC
; (4)AB2=BD·BC| A.3个 | B.2个 | C.1个 | D.0个 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
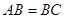 ,且
,且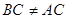 ),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).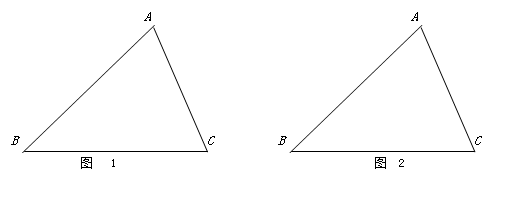 (1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.
(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
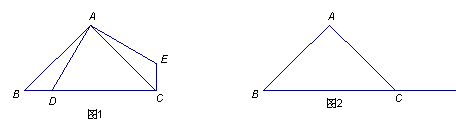
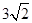 ,试求线段CF长的最大值.
,试求线段CF长的最大值. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com