
 如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分.
如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分. 分析 设AC,GH相交于点O,由四边形ABCD是平行四边形可得AO=CO,AG∥CH,再由平行线的性质可得∠AGO=∠COH,∠GAO=∠HCO,所以可证明△AOG≌△COH,由全等三角形的性质可得GO=OH,即AC与GH互相平分.
解答 证明:设AC,GH相交于点O,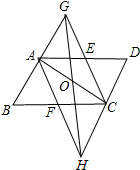
∵四边形ABCD是平行四边形,
∴AO=CO,AG∥CH,
∴∠AGO=∠COH,∠GAO=∠HCO,
在△AOG和△COH中,
$\left\{\begin{array}{l}{∠AGO=∠COH}\\{∠GAO=∠HCO}\\{AO=CO}\end{array}\right.$,
∴△AOG≌△COH(AAS),
∴GO=HO,
∴AC与GH互相平分.
点评 本题考查了平行四边形的判定和性质、全等三角形的判定和性质,证题的关键是通过证明三角形△AOG≌△COH(AAS)得到GO=HO,


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
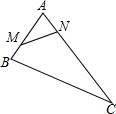 如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似?
如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.
如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
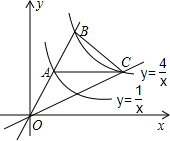 如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3.
如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com