
【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )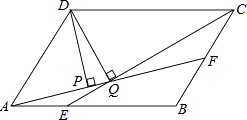
A.3:4
B.![]() :2
:2 ![]()
C.![]() :2
:2 ![]()
D.2 ![]() :
: ![]()
【答案】D
【解析】解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
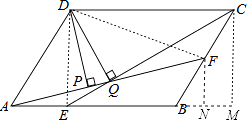
∵根据三角形的面积和平行四边形的面积得:S△DEC=S△DFA= ![]() S平行四边形ABCD,
S平行四边形ABCD,
即 ![]() AF×DP=
AF×DP= ![]() CE×DQ,
CE×DQ,
∴AF×DP=CE×DQ,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠DAB=60°,
∴∠CBN=∠DAB=60°,
∴∠BFN=∠MCB=30°,
∵AB:BC=3:2,
∴设AB=3a,BC=2a,
∵AE:EB=1:2,F是BC的中点,
∴BF=a,BE=2a,
BN= ![]() a,BM=a,
a,BM=a,
由勾股定理得:FN= ![]() a,CM=
a,CM= ![]() a,
a,
AF= ![]() =
= ![]() a,
a,
CE= ![]() =2
=2 ![]() a,
a,
∴ ![]() aDP=2
aDP=2 ![]() aDQ
aDQ
∴DP:DQ=2 ![]() :
: ![]() .
.
故答案为:D.
连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,得出根据三角形的面积和平行四边形的面积得:S△DEC=S△DFA= ![]() S平行四边形ABCD,证得AF×DP=CE×DQ,由AB:BC=3:2,AE:EB=1:2,F是BC的中点,设AB=3a,用含a的代数式分别表示出BC、BF、BE、BN、BM的长,利用勾股定理求出AF、CE的长,代入AF×DP=CE×DQ,即可求出DP:DQ的值。
S平行四边形ABCD,证得AF×DP=CE×DQ,由AB:BC=3:2,AE:EB=1:2,F是BC的中点,设AB=3a,用含a的代数式分别表示出BC、BF、BE、BN、BM的长,利用勾股定理求出AF、CE的长,代入AF×DP=CE×DQ,即可求出DP:DQ的值。


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE。F为AB上一点,且BF=DE,连接FC.
(1)若DE=1,CF=2![]() ,求CD的长。
,求CD的长。
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=600,求证:AF+CE=![]() AC.
AC.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )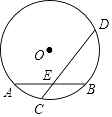
A.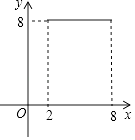
B.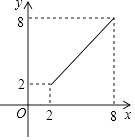
C.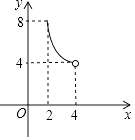
D.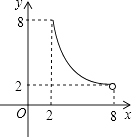
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y= ![]() x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M8坐标为 .
x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M8坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com