练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知Rt△ABC中，∠C=90°，BC=3，AB=5，那么cos∠B的值是 （　　）
    A．$\frac{3}{5}$B．$\frac{3}{4}$C．$\frac{4}{5}$D．$\frac{4}{3}$

    分析 根据余弦等于邻边比斜边，可得答案．

    解答 解：cos∠B=$\frac{BC}{AB}$=$\frac{3}{5}$，
    故选：A．

    点评 本题考查了锐角三角函数的定义，熟记锐角三角函数的定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年浙江省七年级3月月考数学试卷（解析版） 题型：解答题

    已知关于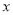， 的方程组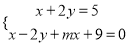

    （1）请写出方程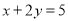的所有正整数解；

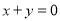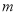    （2）若方程组的解满足，求的值；

    （3）无论实数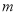取何值，方程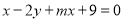总有一个公共解，你能把求出这个公共解吗？

    （4）如果方程组有整数解，求整数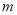的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

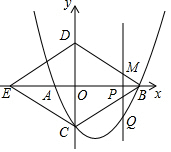    12．抛物线与x轴交于A，B两点，（点B在点A的左侧）且A，B两点的坐标分别为（-2，0）、（8，0），与y轴交于点C（0，-4），连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线L交抛物线于点Q，交BD于点M．
    （1）求抛物线的解析式；
    （2）当点P在线段OB上运动时，试探究m为何值时，四边形CQMD是平行四边形？
    （3）位于第四象限内的抛物线上是否存在点N，使得△BCN的面积最大？若存在，求出N点的坐标，及△BCN面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．阅读资料：
    如图1，在平面直角坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=|x2-x1|2+|y2-y1|2，所以A，B两点间的距离为AB=$\sqrt{{{（{x_2}-{x_1}）}^2}+{{（{y_2}-{y_1}）}^2}}$．
    我们知道，圆可以看成到圆心的距离等于半径的点的集合，如图2，在平面直角坐标系xOy中，A （x，y）为圆上任意一点，则点A到原点的距离的平方为OA2=|x-0|2+|y-0|2，当⊙O的半径OA为r时，⊙O的方程可写为：x2+y2=r2．
    问题拓展：
    如果圆心坐标为P （a，b），半径为r，那么⊙P的方程可以写为（x-a）2+（y-b）2=r2．
    综合应用：
    如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使∠POA=30°，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．
    ①证明AB是⊙P的切线；
    ②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以点Q为圆心，OQ长为半径的⊙Q的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

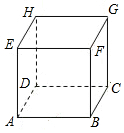    16．如图，一个上方无盖的正方体盒子紧贴地面，一只蚂蚁由盒外AE的中点处出发，沿着盒子面爬行到盒内的点C处，已知正方体的边长为4，问这只蚂蚁爬行的最短距离是10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

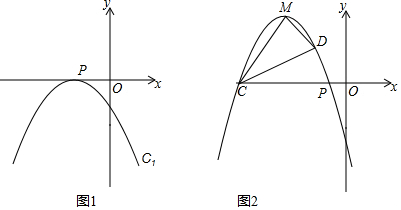    6．已知，抛物线C1：y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$．
    （1）①无论m取何值，抛物线经过定点P（-1，0）；
    ②随着m的取值的变化，顶点M（x，y）随之变化，y是x的函数，则函数C2的关系式为：y=$\frac{1}{2}$（x+1）2；
    （2）如图1，抛物线C1与x轴仅有一个公共点，请在图1画出顶点M满足的函数C2的大致图象，平行于y轴的直线l分别交C1、C2于点A、B，若△PAB为等腰直角三角形，判断直线l满足的条件，并说明理由；
    （3）如图2，二次函数的图象C1的顶点M在第二象限、交x轴于另一点C，抛物线上点M与点P之间一点D的横坐标
    为-2，连接PD、CD、CM、DM，若S△PCD=S△MCD，求二次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AB=5，则CD=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
    （1）直线BF垂直于CE于点F，交CD于点G（如图l），求证：AE=CG；
    （2）直线AH垂直于CE，垂足为H，交CD的延长线于点M（如图2），找出图中与BE相等的线段（不需要添加辅助线），并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．当（a-$\frac{1}{2}$）2+2有最小值时，2a-3=-2．

    查看答案和解析>>

    同步练习册答案