
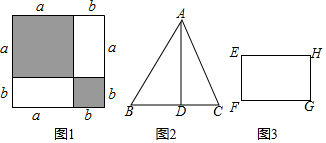
分析 【解决问题】利用作差法比较M与N大小即可;
【拓展延伸】利用作差法比较M与N大小即可;
解答 解:【解决问题】
根据题意得:M=a2+b2,N=ab+ab,
∴M-N=a2+b2-2ab=(a-b)2>0,
∴a≠b,
∴(a-b)2>0,
∴M-N>0,
∴M>N;
【拓展延伸】
在△ABC中,AD⊥BC于D,AD=BC=2x-y,
∴M=$\frac{1}{2}$BC•AD
=$\frac{1}{2}$(2x-y)2
=2x2-2xy+$\frac{1}{2}$y2,
在长方形EFGH中,长EH=2x-$\frac{3}{2}$y,宽EF=y,
∴N=EH•EF
=(2x-$\frac{3}{2}$y)y
=2xy-$\frac{3}{2}$y2,
∴M-N=(2x2-2xy+$\frac{1}{2}$y2)-(2xy-$\frac{3}{2}$y2)
=2x2-2xy+$\frac{1}{2}$y2-2xy+$\frac{3}{2}$y2
=2x2-4xy+2y2
=2(x2-2xy+y2)
=2(x-y)2,
∵x≠y,
∴(x-y)2>0,
∴2(x-y)2>0,
∴M-N>0,
即:M>N.
点评 此题是四边形综合题,主要考查了正方形,三角形,矩形的面积公式,配方法,理解和掌握材料提供的作差法比较代数式大小是解本题的关键.是一道比较简单的题目.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
| 购票人数 | 1-30人 | 31-60人 | 60人以上 |
| 票价 | 无折扣 | 超出30人的部分,票价打八折 | 超出60人的部分,票价打五折 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
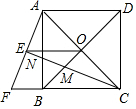 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 固定费用(元) | 免费拨打时间(分钟) | 超出免费时间后单价(元/分钟) | |
| A | 18 | 1500 | 0.1 |
| B | 38 | 4000 | 0.07 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
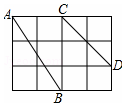 如图,在4×3正方形网格中,每个小正方形的边长都是1
如图,在4×3正方形网格中,每个小正方形的边长都是1查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
下列运算中,正确的是( )
A. 4x+3y=7xy B. 3x2+2=5x2
C. 6xy-4xy=2xy D. 5x2-x2=4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com