
【题目】初三某班同学小代想根据学习函数的经验,探究函数![]() 的图象和性质,下面是他的探究过程,请补充完整:
的图象和性质,下面是他的探究过程,请补充完整:
(1)函数![]() 的自变量的取值范围是 ;
的自变量的取值范围是 ;
(2)下表是函数![]() 与自变量
与自变量![]() 的几组对应值:
的几组对应值:
| -3 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | 7 |
| |
|
| 0.6 | m | 1 | 1.5 | 3 | n | 1.5 | 1 | 0.75 | 0.6 |
|
则m= ,n= ;
(3)在平面直角坐标系xoy中,补全此函数的图象:
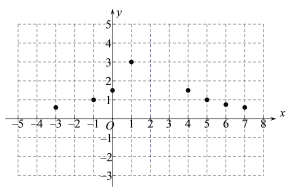
(4)根据函数图象,直接写出不等式![]() 的解集 ;
的解集 ;
(5)若函数![]() 与函数y=x+k图象有三个不同的交点,则k的取值范围是 .
与函数y=x+k图象有三个不同的交点,则k的取值范围是 .
【答案】(1)![]() ;(2)m=0.75,n= 3;(3)在平面直角坐标系xoy中,补全此函数的图象见解析;(4)
;(2)m=0.75,n= 3;(3)在平面直角坐标系xoy中,补全此函数的图象见解析;(4)![]() ;(5)
;(5)![]() .
.
【解析】
(1)根据分母不能为0确定自变量的取值范围;
(2)把x=-2,3分别代入![]() 可求得m,n的值;
可求得m,n的值;
(3)把两组点分别顺次连接可得图象;
(4)作出函数y=x-2的图象,得直线与![]() 的交点的横坐标为x=2+
的交点的横坐标为x=2+![]() .根据图象可得到不等式的解集;
.根据图象可得到不等式的解集;
(5)直线y=x+k与右边曲线总有一个交点,故可求当直线与左边曲线有一个交点时k的值,将直线向上平移就会满足题中有三个交点的条件,从而得到k的取值范围.
(1)根据分母不能为0得│x-2│≠0,解得: ![]() ;
;
(2)将x=-2代入![]() ,得y=0.75,即m=0.75;
,得y=0.75,即m=0.75;
将x=3代入![]() ,得y=3,即n=3;
,得y=3,即n=3;
故答案为:m= 0.75 ,n= 3 ;
(3)如图所示:
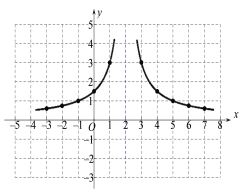
(4)如图,作出函数y=x-2的图象,这条直线与![]() 的交点的横坐标为x=2+
的交点的横坐标为x=2+![]() .
.
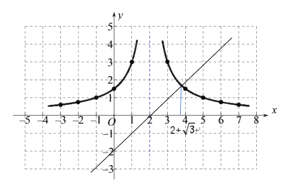
观察图象可得,不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(5)由(4)的结论可知,直线y=x+k与![]() 的图象的右边的曲线总有一个交点,故考虑当x<2时,直线y=x+k与
的图象的右边的曲线总有一个交点,故考虑当x<2时,直线y=x+k与![]() 的图象的左边的曲线的交点情况.
的图象的左边的曲线的交点情况.
∵x<2,∴![]() ,列方程
,列方程![]() =x+k,
=x+k,
整理得![]() ,
,
当![]() 时,方程有唯一解,直线与左边曲线有一个交点,直线继续往上平移,会有两个交点.
时,方程有唯一解,直线与左边曲线有一个交点,直线继续往上平移,会有两个交点.
∴![]()
解得![]() (由图像知
(由图像知![]() 不合题意舍去)
不合题意舍去)
所以当![]() 时,直线y=x+k与
时,直线y=x+k与![]() 共有三个不同的交点.
共有三个不同的交点.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
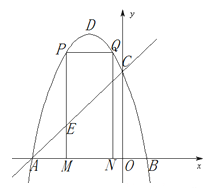
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是![]()
![]()
A. 调查巴南区市民对“巴南区创建国家食品安全示范城市”的了解情况
B. 调查央视节目《国家宝藏》的收视率
C. 调查我校某班学生喜欢上数学课的情况
D. 调查学校所有电子白板的使用寿命
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲、乙两辆货车都要从A地送货到B地,甲车先从A地出发匀速行驶,3小时后,乙车从A地出发,并沿同一路线匀速行驶,当乙车到达B地后立刻按原速返回,在返回途中第二次与甲车相遇。甲车出发的时间记为t (小时),两车之间的距离记为y(千米),y与t的函数关系如图所示,则乙车第二次与甲车相遇时,甲车距离A地___千米.
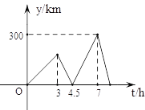
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若![]() ,
,![]() ,则该长方形的面积为__________.
,则该长方形的面积为__________.
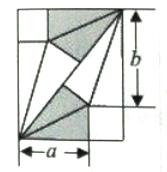
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,对于
,对于![]() 的横长、纵长、纵横比给出如下定义:
的横长、纵长、纵横比给出如下定义:
将![]() 中的最大值,称为
中的最大值,称为![]() 的横长,记作
的横长,记作![]() ;将
;将![]() 中的最大值,称为
中的最大值,称为![]() 的纵长,记作
的纵长,记作![]() ;将
;将![]() 叫做
叫做![]() 的纵横比,记作
的纵横比,记作![]() .
.
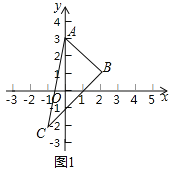
例如:如图![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,则
,则![]() ,
,
所以![]() .
.
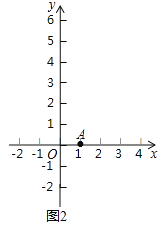
![]() 如图2,点
如图2,点![]() ,
,
![]() 点
点![]() ,
,
则![]() 的纵横比
的纵横比![]() ______
______
![]() 的纵横比
的纵横比![]() ______;
______;
![]() 点F在第四象限,若
点F在第四象限,若![]() 的纵横比为1,写出一个符合条件的点F的坐标;
的纵横比为1,写出一个符合条件的点F的坐标;
![]() 点M是双曲线
点M是双曲线![]() 上一个动点,若
上一个动点,若![]() 的纵横比为1,求点M的坐标;
的纵横比为1,求点M的坐标;
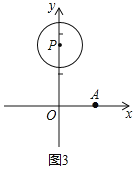
![]() 如图3,点
如图3,点![]() 以
以![]() 为圆心,1为半径,点N是
为圆心,1为半径,点N是![]() 上一个动点,直接写出
上一个动点,直接写出![]() 的纵横比
的纵横比![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某校初二年级的同学乘坐大巴车去北京展览馆参观“砥砺奋进的五年”大型成就展,北京展览馆距离该校12千米,1号车出发3分钟后,2号车才出发,结果两车同时到达,已知2号车的平均速度是1号车的平均速度的1.2倍,求2号车的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com