
 如图,5个同样大小的正方形拼成一个长方形,求∠ABC+∠ADC+∠ACB的度数.
如图,5个同样大小的正方形拼成一个长方形,求∠ABC+∠ADC+∠ACB的度数. 分析 利用勾股定理分别计算出△ACD和△ADB的各个边长,根据有三边比值相等的两三角形相似可判定△ACD和△ADB相定理即可求出似,再根据相似三角形的性质:对应角相等和三角形外角和定理即可求出∠ABC+∠ADC+∠ACB的度数.
解答 解:设每个小正方形的边长为1,
由勾股定理得:AC=$\sqrt{2}$,AD=$\sqrt{5}$,AB=$\sqrt{10}$,
又∵DC=1,BD=5,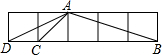
∴$\frac{AD}{BD}$=$\frac{\sqrt{5}}{5}$,$\frac{AC}{AB}=\frac{\sqrt{2}}{\sqrt{10}}=\frac{\sqrt{5}}{5}$,$\frac{CD}{AD}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{AD}{BD}$=$\frac{AC}{AB}=\frac{CD}{AD}$,
∴△ADC∽△BDA,
∴∠DAC=∠ABD,
∵∠ACB=45°,
∴∠ACB=∠DAC+∠ADB=45°,
∴∠ABC+∠ADC+∠ACB=90°.
点评 本题考查了相似三角形的判定和相似三角形的性质以及勾股定理的运用和三角形的外角和不相邻的两内角之间的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某水库蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图,请根据此图回答下列问题:
如图是某水库蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图,请根据此图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com