
分析 (1)直接利用度分秒之间的换算关系求出即可;
(2)直接利用度分秒之间的换算关系求出即可;
(3)设这个角为x,则补角为(180°-x),余角为(90°-x),再由补角比它的余角的3倍多30°,可得方程,解出即可.
解答 解:(1)(1)131°28′-51°32′15〞
=182°60′15″
=183°15″;
(2)58°38′27〞+47°42′40〞
=105°80′67″
=106°21′7″;
(3)设这个角为x,则补角为(180°-x),余角为(90°-x),
由题意得,180°-x=3(90°-x)+30°,
解得:x=60.
即这个角的度数是60°.
点评 本题考查了度分秒转换和余角、补角的知识,解答本题的关键是掌握互余的两角之和为90°,互补的两角之和为180°.


科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
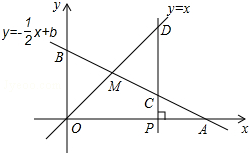 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
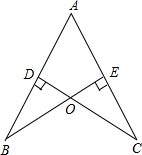 如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个函数图象都经过第四象限 | |
| B. | 两个函数图象有两个公共点 | |
| C. | 两个函数在自变量的取值范围内y都随x的增大而增大 | |
| D. | 在第二象限内,函数y=x+1的值小于函数y=-$\frac{1}{x}$的值 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
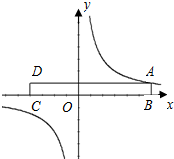 如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).
如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.
如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com