
【题目】△ABC中,AC=BC,∠ACB=α,点D是平面内不与点A和点B重合的一点,连接DB,将线段DB绕点D顺时针旋转α得到线段DE,连接AE、BE、CD.
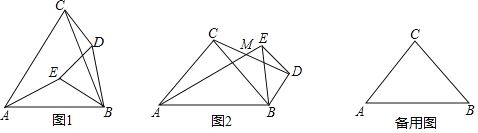
(1)如图①,点D与点A在直线BC的两侧,α=60°时,![]() 的值是 ;直线AE与直线CD相交所成的锐角的度数是 度;
的值是 ;直线AE与直线CD相交所成的锐角的度数是 度;
(2)如图②,点D与点A在直线BC两侧,α=90°时,求![]() 的值及直线AE与直线CD相交所成的锐角∠AMC的度数;
的值及直线AE与直线CD相交所成的锐角∠AMC的度数;
(3)当α=90°,点D在直线AB的上方,S△ABD=![]() S△ABC,请直接写出当点C、D、E在同一直线上时,
S△ABC,请直接写出当点C、D、E在同一直线上时,![]() 的值.
的值.
【答案】(1)1,60;(2)∠AMC=45°;(3)![]() 的值为2﹣
的值为2﹣![]() 或2+
或2+![]() .
.
【解析】
(1)延长AE,CD交于点H,根据旋转的性质可知DE=BD,∠BDE=60°,从而可知△BDE,从而可证△ABE≌△CBD,从而可知![]() ,再根据角的关系即可求出∠AHB;
,再根据角的关系即可求出∠AHB;
(2)先证△ABE∽△CBD,可以得到![]() ,∠BAE=∠BCD,继而可以求出∠AMC的度数;
,∠BAE=∠BCD,继而可以求出∠AMC的度数;
(3)分两种情况讨论即可:①点D,点A在直线BC两侧,②点A,点D在直线BC同侧.
(1)如图1,延长AE,CD交于点H,
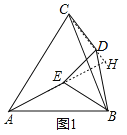
∵将线段DB绕点D顺时针旋转α得到线段DE,
∴DE=BD,∠BDE=60°,
∴△BDE是等边三角形,
∴BD=BE,∠DBE=60°,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,且BE=BD,AB=BC,
∴△ABE≌△CBD(SAS)
∴AE=CD,∠DCB=∠BAE,
∴![]() =1,
=1,
∵∠BAC+∠ACB=120°,
∴∠BAE+∠CAE+∠ACB=120°,
∴∠CAE+∠ACB+∠BCD=120°
∴∠CAE+ACH=120°,
∴∠AHB=60°,
故答案为:1,60.
(2)∵AC=BC,∠ACB=90°,
∴AB=![]() BC,∠ABC=45°,
BC,∠ABC=45°,
∵将线段DB绕点D顺时针旋转90°得到线段DE,
∴DE=BD,∠BDE=90°,
∴BE=![]() BD,∠DBE=45°,
BD,∠DBE=45°,
∴∠DBE=∠ABC,
∴∠ABE=∠CBD,且![]() ,
,
∴△ABE∽△CBD,
∴![]() ,∠BAE=∠BCD,
,∠BAE=∠BCD,
∵∠BAC+∠ACB=135°=∠ACB+∠CAM+∠BAE,
∴∠ACB+∠CAM+∠BCD=∠CAM+∠ACM=135°,
∴∠AMC=45°;
(3)①若点D,点A在直线BC两侧,如图3,分别取AC,BC中点G,H,连接GH,
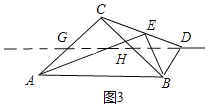
∵![]() ,
,
∴点D在直线GH上,
∵∠ACB=∠BDE=90°,AC=BC,DE=BD,
∴∠CAB=∠CBA=45°,∠DEB=∠DBE=45°,BE=![]() BD,
BD,
∵点G,点H分别是AC,BC的中点,
∴GH∥AB,
∴∠DHB=∠ABC=45°,
∵点C、E、D三点共线,
∴∠CDB=90°,且点H是BC中点,
∴DH=CH=BH,
∴∠HCD=∠HDC,且∠HCD+∠HDC=∠BHD=45°,
∴∠HCD=∠HDC=22.5°,
∵∠BED=∠BCE+∠CBE=45°,
∴∠BCE=∠CBE=22.5°,
∴BE=CE=![]() BD,
BD,
∴CD=CE+DE=(![]() +1)BD,
+1)BD,
∴![]() ;
;
②若点A,点D在直线BC同侧,如图4,分别取AC,BC中点G,H,连接GH,
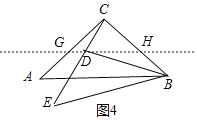
∵![]() ,
,
∴点D在直线GH上,
∵∠ACB=∠BDE=90°,AC=BC,DE=BD,
∴∠CAB=∠CBA=45°,∠DEB=∠DBE=45°,BE=![]() BD,
BD,
∵点G,点H分别是AC,BC的中点,
∴GH∥AB,
∴∠DHC=∠ABC=45°,
∵点C、E、D三点共线,
∴∠CDB=90°,且点H是BC中点,
∴DH=CH=BH,
∴∠HBD=∠HDB,且∠HBD+∠HDB=∠CHD=45°,
∴∠HBD=∠HDB=22.5°,
∵∠ECB=67.5°,∠EBC=∠EBD+∠DBC=67.5°,
∴∠BCE=∠CBE=67.5°,
∴BE=CE=![]() BD,
BD,
∴CD=CE﹣DE=(![]() ﹣1)BD,
﹣1)BD,
∴![]() ,
,
综上所述:![]() 的值为
的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).
(1)小红摸出标有数3的小球的概率是多少?.
(2)请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.
(3)求点P(x,y)在函数y=﹣x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
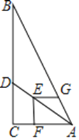
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF = EG,则CD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于点G,连接AF,给出下列结论:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,点E在AD边上且不与点A和点D重合,点O是对角线BD的中点,当△OED是等腰三角形时,AE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE
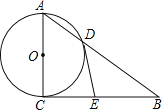
(1)求证:△DBE是等腰三角形
(2)求证:△COE∽△CAB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面图形S,点P、Q是S上任意两点,我们把线段PQ的长度的最大值称为平面图形S的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
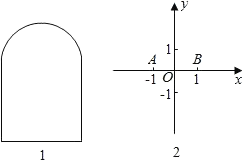
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
(2)如图2,在平面直角坐标系中,已知点A(﹣1,0)、B(1,0),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的宽距为d.
①若d=2,求点C所在的区域的面积;
②若点C在⊙M上运动,⊙M的半径为1,圆心M在过点(0,2)且与y轴垂直的直线上.对于⊙M上任意点C,都有5≤d≤8,直接写出圆心M的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
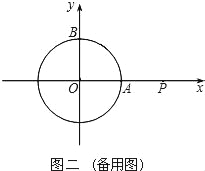
【题目】以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
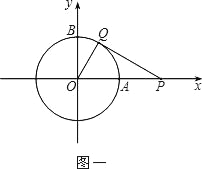
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com