
(1)式子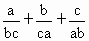 的值能否为0?为什么?
的值能否为0?为什么?
(2)式子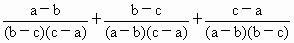 的值能否为0?为什么?
的值能否为0?为什么?
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
| 次数n | 2 | 1 |
| 速度x | 40 | 60 |
| 指数Q | 420 | 100 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(河北卷)数学(带解析) 题型:解答题
某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q =" W" + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
| 次数n | 2 | 1 |
| 速度x | 40 | 60 |
| 指数Q | 420 | 100 |
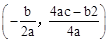
查看答案和解析>>
科目:初中数学 来源:2013年河北省中考数学试卷(解析版) 题型:解答题
| 次数n | 2 | 1 |
| 速度x | 40 | 60 |
| 指数Q | 420 | 100 |
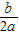 ,
,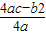 )
)查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(河北卷)数学(解析版) 题型:解答题
某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q =" W" + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
|
次数n |
2 |
1 |
|
速度x |
40 |
60 |
|
指数Q |
420 |
100 |
(1)用含x和n的式子表示Q;
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com