
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由BC⊥AF可得∠A+∠B=90°,又因为∠A+∠1=90°,根据同角的余角相等可证∠B=∠1,从而AB∥DE.
(2)分①点P在A,D之间时,②当点P在C,D之间时,③点P在C,F之间时三种情况,分别过P作PG∥AB,根据平行线的性质求解即可.
(1)如图1,∵BC⊥AF于点C,
∴∠A+∠B=90°,
又∵∠A+∠1=90°,
∴∠B=∠1,
∴AB∥DE.
(2)如图2,当点P在A,D之间时,过P作PG∥AB,
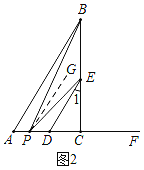
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG+∠EPG=∠ABP+∠DEP;
如图所示,当点P在C,D之间时,过P作PG∥AB,
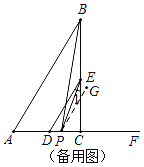
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG﹣∠EPG=∠ABP﹣∠DEP;
如图所示,当点P在C,F之间时,过P作PG∥AB,
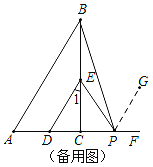
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠EPG﹣∠BPG=∠DEP﹣∠ABP.


科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出): 
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA表示的方向是北偏东15°,射线OB表示的方向是北偏西40°.
(1)若∠AOC=∠AOB,则射线OC表示的方向是 ;
(2)若射线OD是射线OB的反向延长线,则射线OD表示的方向是 ;
(3)∠BOD可以看作是由OB绕点O逆时针方向旋转至OD形成的角,作∠BOD的平分线OE;
(4)在(1),(2),(3)的条件下,求∠COE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数的卡片,请你分别按要求抽出卡片,写出符合要求的算式:
![]()
(1)从中取出2张卡片,使这2张卡片上的数的乘积最大;
(2)从中取出2张卡片,使这2张卡片上的数相除的商最小;
(3)从中取出2张卡片,使这2张卡片上的数通过有理数的运算后得到的结果最大;
(4)从中取出4张卡片,使这4张卡片通过有理数的运算后得到的结果为24.(写出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1,S2,S3,S4,若MN∥AB∥CD,EF∥DA∥CB,则有( )
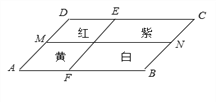
A. S1=S4 B. S1+S4=S2+S3 C. S1S4=S2S3 D. 都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20 ![]() m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:
m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据: ![]() 1.414,
1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com