练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图，四边形ABCD和EFGC都是正方形，写出表示阴影部分面积的代数式．

    分析 阴影部分面积可视为大小正方形减去空白部分（即△ABD和△BFG），把对应的三角形面积代入即可得出．

    解答 解：阴影部分面积S=a2+b2-$\frac{1}{2}$a2-$\frac{1}{\;}$（a+b）b=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$ab-$\frac{1}{2}$b2=$\frac{1}{2}$a2-$\frac{1}{2}$ab+$\frac{1}{2}$b2．

    点评 本题考查列代数式．要求对图形间的关系准确把握，找到阴影部分的面积是哪些规则图形的面积差是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

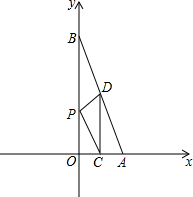    11．如图，一次函数y=kx+b的图象与x，y轴分别交于A（2，0）和B（0，8）点C，D分别在OA，AB上，且C（1，0），D（1，m）．
    （1）直接写出该函数的表达式和m的值．
    （2）若P为OB上的一个动点，试求PC+PD的最小值．
    （3）连接CD，若P为y轴上的一动点，△PCD为等腰三角形，试求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．实数a，b在数轴上的位置如图所示，那么化简|a-b|-$\sqrt{a^2}$的结果是（　　）
    A．-bB．a2+2C．$\sqrt{a+2}$D．$\sqrt{{a^2}+2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图所示，观察图形1+3+5+7+9+11=（6）2，由此你能退出从1开始n个连续奇数之和是多少吗？选择几个n的值，用计算器验证一下．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．观察右面由“※”组成的图案和算式．解答问题．
    1+3=4=22；
    1+3+5=9=32；
    1+3+5+7=16=42；
    1+3+5+7+9=25=52．
    （1）请猜想：1+3+5+7+9+…+19=102：
    （2）请猜想：1+3+5+7+9+…+（2n-1）=n2；
    （3）请用上述规律计算：103+105+107+…+2013+2015．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，AB是半圆O的直径，点C、D、E、F在半圆上，AC=CD=DE=EF=FB，则∠COF=（　　）
    A．90°B．100°C．108°D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

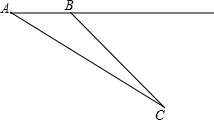    13．随着课程改革的不断深入，对话交流、师生共同探索已成课堂常态，下面的问题取自课堂实录：（在本题计算中sin37°=$\frac{3}{5}$，cos37°=$\frac{4}{5}$，tan37°=$\frac{3}{4}$，cot37°=$\frac{4}{3}$）
    老师首先给出（1）：如图，在一次直行中观察道路一边的某建筑物C，在A点处观察到看该建筑物的视线和公路的夹角为37°，继续直行50米到达B后发现看该建筑物的视线和公路的夹角变成了45°，求该建筑物C离开公路的距离（请你一起完成）
    然后老师又给出变式（2）：如果我们在上述问题中删去“如图”两个字，其它不变，这时，问题的答案是否有变化？如果有变化，请画出草图并求出答案（请你一起完成）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．20022016的末位数字是多少？为了解决这个问题，不妨从特殊数的幂的个位数字中发现规律：
    21=2，22=4，23=8，24=16，
    25=24+1=32，26=24+2=64，27=24+3=128，28=24+4=258．
    24k+1个位数字为2，24k+2个位数字为4，24k+3个位数字为8，24（k+1）个位数字为6．
    从上述数据中发现，底数为2，指数分别为（4k+1），（4k+2），（4k+3），4k+4时，幂的末位数分别为2，4，8，6，又20022016=20024×504=24×504×10014×504，因此它与24的个位数字相同；幂20022016的末位数字是6．
    你能推出32015个位上的数字是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．化简：
    （1）$\frac{1}{2}$（8x-6y）+3（y-$\frac{x}{3}$）；
    （2）3（2x-3y）-2（3x-2y）；
    （3）2（x2-3xy）-3（y2-2xy）．

    查看答案和解析>>

    同步练习册答案