
【题目】如图①,已知抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
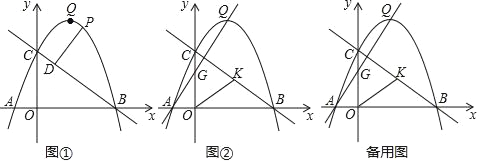
(1)求直线BC的解析式;
(2)点P是直线BC上方抛物线上的一点,过点P作PD⊥BC于点D,在直线BC上有一动点M,当线段PD最大时,求PM+![]() MB最小值;
MB最小值;
(3)如图②,直线AQ交y轴于G,取线段BC的中点K,连接OK,将△GOK沿直线AQ平移得△G′O'K′,将抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() .(2)
.(2)![]() ;(3)点G′坐标为(
;(3)点G′坐标为(![]() )或(3,5
)或(3,5![]() )或(5,
)或(5,![]() )或(4,
)或(4,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)利用待定系数法求出B,C两点坐标即可解决问题.
(2)因为∠DPM是定值,推出当PM的值最大时,PD的值最大,构建二次函数求出PD最大时,点P坐标,在y轴上取一点G,使得sin∠GBC=![]() ,作GK⊥BC于K,因为PM+
,作GK⊥BC于K,因为PM+![]() BM=PM+ME,把问题转化为:当P.M,E共线,且PE⊥BG时,PM+PE的值最小,由此求出点E坐标即可解决问题.
BM=PM+ME,把问题转化为:当P.M,E共线,且PE⊥BG时,PM+PE的值最小,由此求出点E坐标即可解决问题.
(3)分三种情形构建方程即可解决问题.
解:(1)令y=0,﹣![]() x2+
x2+![]() x+2
x+2![]() =0,解得x=﹣1和4,
=0,解得x=﹣1和4,
∴A(﹣1,0),B(4,0),
令x=0,y=2![]() ,
,
∴C(0,2![]() ),
),
设直线BC是解析式为y=kx+b,则有![]() ,解得
,解得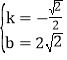 ,
,
∴直线BC的解析式为y=﹣![]() x+2
x+2![]() .
.
(2)如图1中,作PM∥y轴交BC于M.

∵∠DPM是定值,
∴当PM的值最大时,PD的值最大,设P(m,﹣![]() m2+
m2+![]() m+2
m+2![]() ),则M(m,﹣
),则M(m,﹣![]() m+2
m+2![]() ),
),
∴PM=﹣![]() m2+2
m2+2![]() m=﹣
m=﹣![]() (m﹣2)2+2
(m﹣2)2+2![]() ,
,
∵﹣![]() <0,
<0,
∴m=2时,PM的值有最大值,即PD的值最大,此时P(2,3![]() ).
).

在y轴上取一点G,使得sin∠GBC=![]() ,作GK⊥BC于K,
,作GK⊥BC于K,
∵sin∠GBK=![]() =
=![]() ,设GK=k,BG=3k,则BK=2
,设GK=k,BG=3k,则BK=2![]() k,
k,
∵∠GCK=∠BCO,∠GKC=∠BOC=90°,
∴△CKG∽△COB,
∴![]() ,
,
∴![]() ,
,
∴CK=![]() k,CG=
k,CG=![]() k,
k,
∵CK+BK=BC,
∴![]() k+2
k+2![]() k=2
k=2![]() ,
,
∴k=![]() ,
,
∴OG=OC﹣CG=![]() ,
,
∴G(0,![]() ),
),
∴直线BG的解析式为y=﹣![]() x+
x+![]() ,
,
∵PM+![]() BM=PM+ME,
BM=PM+ME,
∴当P.M,E共线,且PE⊥BG时,PM+PE的值最小,
∵PE⊥BG,
∴直线PE的解析式为y=y=![]() x﹣2
x﹣2![]() ,
,
由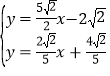 ,解得
,解得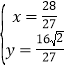 ,
,
∴E(![]() ),
),
∴PE=![]() ,
,
∴PM+![]() BM的最小值为
BM的最小值为![]() .
.
(3)如图3中,存在.

由题意A(﹣1,0),Q(![]() ,
,![]() ),Q′(4,
),Q′(4,![]() ),C(0,2
),C(0,2![]() ),K(2,
),K(2, ![]() ),
),
∴直线AQ的解析式为y=![]() x+
x+![]() ,
,
∴G(0,![]() ),
),
设G′(a,![]() a+
a+![]() ),则K′(a+2,
),则K′(a+2,![]() a+
a+![]() ),
),
当Q′G′=Q′K′时,(a﹣4)2+(![]() a﹣5
a﹣5![]() )2=(a﹣2)2+(
)2=(a﹣2)2+(![]() a﹣
a﹣![]() )2,
)2,
解得a=![]() .
.
此时G(![]() ).
).
当Q′G′=G′K′时,(a﹣4)2+(![]() a﹣5
a﹣5![]() )2=22+(
)2=22+(![]() )2,
)2,
整理得:a2﹣8a+15=0,
解得a=3和5,
此时G′((3,5![]() )或(5,
)或(5,![]() ),
),
当Q′K′=G′K′时,(a﹣2)2+(![]() a﹣
a﹣![]() )2=22+(
)2=22+(![]() )2,
)2,
整理得:3a2﹣8a+15=0,
解得a=4和![]() ,
,
此时G′(4,![]() )或(
)或(![]() ,
,![]() ),
),
综上所述,满足条件的点G′坐标为(![]() )或(3,5
)或(3,5![]() )或(5,
)或(5,![]() )或(4,
)或(4,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴交于点(-2,0)、(
的图像与x轴交于点(-2,0)、(![]() ),且
),且![]() ,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委计划在元且期间组织优秀团员到敬老院去服务,现选出了10名优秀团员参加服务,其中男生6人,女生4人.
![]() 若从这10人中随机选一人当队长,求选中女生当队长的概率;
若从这10人中随机选一人当队长,求选中女生当队长的概率;
![]() 现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长
现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长![]() 试问这个游戏公平吗?请用树状图或列表法说明理由.
试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017
首先设S=1+2+22+23+24+…+22017 ① 则2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在数列求和中,我们称之为:“错位相减法”
请你根据上面的材料,解决下列问题
(1)求1+3+32+33+34+…+32019的值
(2)若a为正整数且![]() ,求
,求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于世界人口增长、水污染以及水资源浪费等原因,全世界面临着淡水资源不足的问题,我国是世界上严重缺水的国家之一,人均占水量仅为2400m3左右,我国已被联合国列为13个贫水国家之一,合理利用水资源是人类可持续发展的当务之急,而节约用水是水资源合理利用的关键所在,是最快捷、最有效、最可行的维护水资源可持续利用的途径之一,为了调查居民的用水情况,有关部门对某小区的20户居民的月用水量进行了调查,数据如下:(单位:t)
6.7 | 8.7 | 7.3 | 11.4 | 7.0 | 6.9 | 11.7 | 9.7 | 10.0 | 9.7 |
7.3 | 8.4 | 10.6 | 8.7 | 7.2 | 8.7 | 10.5 | 9.3 | 8.4 | 8.7 |
整理数据 按如下分段整理样本数据并补至表格:(表1)
用水量x(t) | 6.0≤x<7.5 | 7.5≤x<9.0 | 9.0≤x<10.5 | 10.5≤x<12 |
人数 | a | 6 | b | 4 |
分析数据,补全下列表格中的统计量;(表2)
平均数 | 中位数 | 众数 |
8.85 | c | d |
得出结论:
(1)表中的a= ,b= ,c= ,d= .
(2)若用表1中的数据制作一个扇形统计图,则9.0≤x<10.5所示的扇形圆心角的度数为 度.
(3)如果该小区有住户400户,请根据样本估计用水量在6.0≤x<9.0的居民有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E在线段BC上,△ADE是等边三角形,且∠BAC=120°
(1)求证:△ABD∽△CAE;
(2)若BD=2,CE=8,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在半圆O上,半径OB=2![]() ,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )

A. 5B. 6C. 7D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com