
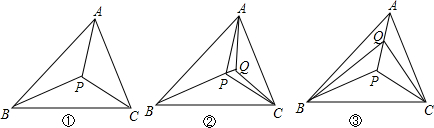
���� ̽���������������ڲ����㹲���벻����������������ָ�ʾ��ͼ������ֳɵIJ��ּ��ɣ�
̽���ģ�����ǰ����̽�����ѷ��֣��������ڲ�ÿ����һ���㣬�ָ������2���֣����ݴ˹���д����m+3������ָ�IJ��������ɣ�
̽����չ�������������ε�����д�������������ɵý⣻
�����������ݹ��ɣ�����Ӧ�ĵ�������m��n�������ɵý⣻
ʵ��Ӧ�ã��ѹ�ʽ�е���Ӧ����ĸ�����ɾ�������ݣ�Ȼ����㼴�ɵý⣮
��� 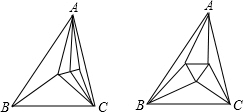 �⣺̽��������ͼ���������ڲ������㹲���벻����ʱ���ֳ���7���֣�
�⣺̽��������ͼ���������ڲ������㹲���벻����ʱ���ֳ���7���֣�
�ָ�ʾ��ͼ���𰸲�Ψһ����
̽���ģ��������ڲ�1����ʱ�����ָ��3���֣�3=3+2��1-1����
�������ڲ�2����ʱ�����ָ��5���֣�5=3+2��2-1����
�������ڲ�3����ʱ�����ָ��7���֣�7=3+2��3-1����
����
���ԣ��������ڲ���m����ʱ��3+2��m-1����2m+1��
̽����չ���ı��ε�4����������ڲ���m���㣬
��ָ�ɵIJ��ص��������εĸ���Ϊ��4+2��m-1����2m+2��
��������n+2��m-1����2m+n-2��
ʵ��Ӧ�ã���n=8��m=2012������������ʽ����
2m+n-2
=2��2012+8-2
=4024+8-2
=4030��
���� ���⿼����ͼ�εı仯���ɵ����⣬������Ŀ��Ϣ������ǰ�ĸ�̽���õ�ÿ��һ���㣬�������εĸ�������2�ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{{2}^{2}+{3}^{2}}$=2+3 | B�� | 3$\sqrt{2}$+5$\sqrt{3}$=8$\sqrt{6}$ | ||
| C�� | $\sqrt{1{5}^{2}-1{2}^{2}}$=$\sqrt{15+12}$��$\sqrt{15-12}$ | D�� | $\sqrt{4\frac{1}{2}}$=2$\sqrt{\frac{1}{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | -$\frac{1}{4}$ | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
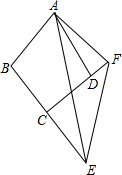 ��ͼ�����ı���ABCD�У���B+��ADC=180�㣬AB=AD��E��F�ֱ��DZ�BC��CD�ӳ����ϵĵ㣬�ҡ�EAF=$\frac{1}{2}$��BAD����֤��EF=BE-FD��
��ͼ�����ı���ABCD�У���B+��ADC=180�㣬AB=AD��E��F�ֱ��DZ�BC��CD�ӳ����ϵĵ㣬�ҡ�EAF=$\frac{1}{2}$��BAD����֤��EF=BE-FD���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com