
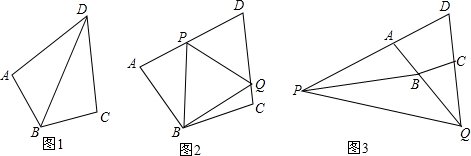
���� ��1����ͼ1������HL֤������ֱ��������ȫ�ȣ�Rt��BAD��Rt��BCD�������Ӧ����ȣ�AD=DC=2��
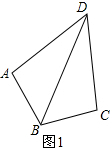
��2����ͼ2���ӳ�DC����������һ��K��ʹ��CK=AP������BK��ͨ��֤��BPA�ա�BCK��SAS���õ�����1=��2��BP=BK��Ȼ����ȫ�������Ρ�PBQ�ա�BKQ��á�PBQ=$\frac{1}{2}$��ABC�������֪��������ABC+��ADC=180�㡱���ɵõ����ۣ�
��3����ͼ3����CD�ӳ�������һ��K��ʹ��KC=AP������BK������ȫ�������Σ���BPA�ա�BCK��SAS�����ɸ�ȫ�������ε����ʺ�ȫ�������ε��ж�����SSS֤�ã���PBQ�ա�BKQ�������Ӧ����ȣ���PBQ=��KBQ������ı��ε��ڽǺ���360�ȿ����Ƶã���PBQ=90��+$\frac{1}{2}$��ADC��
���  ��1���⣺��ͼ1���ߡ�ABC+��ADC=180�㣬��BAD=90�㣬
��1���⣺��ͼ1���ߡ�ABC+��ADC=180�㣬��BAD=90�㣬
���BCD=90�㣬
��Rt��BAD��Rt��BCD��
$\left\{\begin{array}{l}{BD=BD}\\{AB=BC}\end{array}\right.$��
��Rt��BAD��Rt��BCD��HL����
��AD=DC=7��
��DC=7��
��2����ͼ2���ӳ�DC����������һ��K��ʹ��CK=AP������BK����PBQ=��ABP+��QBC��
�ߡ�ABC+��ADC=180�㣬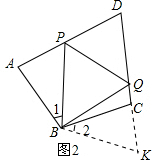
���BAD+��BCD=180�㣮
�ߡ�BCD+��BCK=180�㣬
���BAD=��BCK��
�ڡ�BPA�͡�BCK�У�
$\left\{\begin{array}{l}{AP=CK}\\{��BAP=��BCK}\\{AB=BC}\end{array}\right.$��
���BPA�ա�BCK��SAS����
���1=��2��BP=BK��
��PQ=AP+CQ��
��PQ=QK��
���ڡ�PBQ�͡�BKQ�У�
$\left\{\begin{array}{l}{BP=BK}\\{BQ=BQ}\\{PQ=KQ}\end{array}\right.$��
���PBQ�ա�BKQ��SSS����
���PBQ=��KBQ��
���PBQ=��2+��CBQ=��1+��CBQ�� ���PBQ=��ABP+��QBC��
���PBQ=��ABP+��QBC��
��3����PBQ=90��+$\frac{1}{2}$��ADC��
��ͼ3����CD�ӳ�������һ��K��ʹ��KC=AP������BK��
�ߡ�ABC+��ADC=180�㣬
���BAD+��BCD=180�㣮
�ߡ�BAD+��PAB=180�㣬
���PAB=��BCK��
�ڡ�BPA�͡�BCK�У�
$\left\{\begin{array}{l}{AP=CK}\\{��BAP=��BCK}\\{AB=BC}\end{array}\right.$��
���BPA�ա�BCK��SAS����
���ABP=��CBK��BP=BK��
���PBK=��ABC��
��PQ=AP+CQ��
��PQ=QK��
�ڡ�PBQ�͡�BKQ�У�
$\left\{\begin{array}{l}{BP=BK}\\{BQ=BQ}\\{PQ=KQ}\end{array}\right.$��
���PBQ�ա�BKQ��SSS����
���PBQ=��KBQ��
��2��PBQ+��PBK=2��PBQ+��ABC=360�㣬
��2��PBQ+��180��-��ADC��=360�㣬
���PBQ=90��+$\frac{1}{2}$��ADC��
���� ���⿼����ȫ�������ε��ж������ʣ���Ӧ��ȫ�������ε��ж�ʱ��Ҫע�������μ�Ĺ����ߺ����ǣ���Ҫʱ�����ʵ������߹��������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
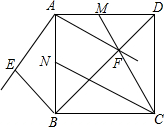 ��ͼ����������ABCD�У�AB=2$\sqrt{2}$������BAD���ŵ�A˳ʱ����ת���㣨0������45�����õ���B��AD�䣬���й���B����Խ���BD��ֱ��ֱ�߽�����AB���ڵ�E������AD����Խ���BD���ڵ�F������CF�����ӳ���AD�ڵ�M������BCM�Ľ�ƽ���߽�AB�ڵ�N��������S�ı���AEBF=$\sqrt{2}$S��CDMʱ���߶�BN�ij���Ϊ2$\sqrt{3}$-2��
��ͼ����������ABCD�У�AB=2$\sqrt{2}$������BAD���ŵ�A˳ʱ����ת���㣨0������45�����õ���B��AD�䣬���й���B����Խ���BD��ֱ��ֱ�߽�����AB���ڵ�E������AD����Խ���BD���ڵ�F������CF�����ӳ���AD�ڵ�M������BCM�Ľ�ƽ���߽�AB�ڵ�N��������S�ı���AEBF=$\sqrt{2}$S��CDMʱ���߶�BN�ij���Ϊ2$\sqrt{3}$-2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a8��a2=a4 | B�� | a3+a3=a6 | C�� | ��a3��3=a6 | D�� | ��-a��2•��-a��3=-a5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com