
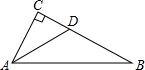
 如图,在△ABC中,∠C=90°,∠CAB的角平分线AD交BC于点D,若BC=20,BD:CD=3:2,则点D到AB的距离为( )
如图,在△ABC中,∠C=90°,∠CAB的角平分线AD交BC于点D,若BC=20,BD:CD=3:2,则点D到AB的距离为( )| A. | 8 | B. | 12 | C. | 4 | D. | 20 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上.
小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
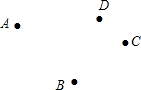 已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.
已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
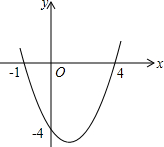 二次函数y=ax2+bx+c的图象如图所示,求:
二次函数y=ax2+bx+c的图象如图所示,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com