
分析 利用二次函数的解析式可求得开口方向、对称轴和顶点坐标.
解答 解:
(1)∵y=$\frac{1}{6}{x}^{2}$-7,
∴开口向上,对称轴为y轴,顶点坐标为(0,-7);
(2)∵y=-$\frac{1}{5}(x+1)^{2}$,
∴开口向上,对称轴为x=-1,顶点坐标为(-1,0);
(3)∵y=1-($\frac{1}{2}$-x)2y=-(x-$\frac{1}{2}$)2+1,
∴开口向下,对称轴为x=$\frac{1}{2}$,顶点坐标为($\frac{1}{2}$,1).
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,顶点坐标为(h,k),对称轴为x=h.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
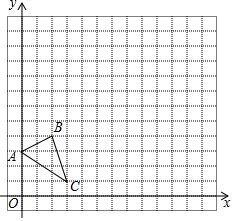 如图,
如图,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com