
 如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.分析 (1)只要证明EB是⊙O的切线,利用切线长定理可知EC=EB,即可解决问题.
(2)连接CF、CO、AC.在Rt△CFH中,由CF=6,sin∠FCH=$\frac{3}{5}$,推出FH=CF•sin∠FCH=$\frac{18}{5}$,CH=$\sqrt{C{F}^{2}-F{H}^{2}}$=$\frac{24}{5}$,设OC=OF=x,在Rt△COH中,由OC2=CH2+OH2,可得x2=($\frac{24}{5}$)2+(x-$\frac{18}{5}$)2,解得x=5,推出OH=$\frac{7}{5}$,再利用三角形中位线定理证明AC=2OH即可解决问题.
解答 (1)证明:∵BE⊥OB,
∴BE是⊙O的切线,∵EC是⊙O的切线,
∴EC=EB,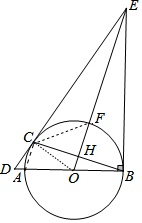
∴∠ECB=∠EBC.
(2)解:连接CF、CO、AC.
∵EB=EC,OC=OB,
∴EO⊥BC,
∴∠CHF=∠CHO=90°,
在Rt△CFH中,∵CF=6,sin∠FCH=$\frac{3}{5}$,
∴FH=CF•sin∠FCH=$\frac{18}{5}$,CH=$\sqrt{C{F}^{2}-F{H}^{2}}$=$\frac{24}{5}$,
设OC=OF=x,
在Rt△COH中,∵OC2=CH2+OH2,
∴x2=($\frac{24}{5}$)2+(x-$\frac{18}{5}$)2,
∴x=5,
∴OH=$\frac{7}{5}$,
∵OH⊥BC,
∴CH=HB,∵OA=OB,
∴AC=2OH=$\frac{14}{5}$.
点评 本题考查切线的性质和判定、解直角三角形、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
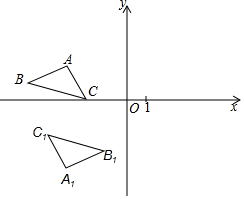 如图,在平面直角坐标系中,△ABC和△A1B1C1关于点D成中心对称.
如图,在平面直角坐标系中,△ABC和△A1B1C1关于点D成中心对称.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
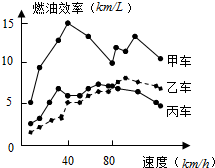 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )| A. | 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 | |
| B. | 以低于80km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少 | |
| C. | 以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油 | |
| D. | 以80km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分组 | 频数累计 | 频数 | 频率 |
| 60.5~70.5 | 正 | 3 | a |
| 70.5~80.5 | 正正 | 6 | 0.12 |
| 80.5~90.5 | 正正 | 9 | 0.18 |
| 90.5~100.5 | 正正正正 | 17 | 0.34 |
| 100.5~110.5 | 正正 | b | 0.2 |
| 110.5~120.5 | 正 | 5 | 0.1 |
| 合计 | 50 | 1 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,AB=4,取CD中点O,以O为圆心OD为半径作圆交AD于E,交BC的延长线交于点F,
如图,在菱形ABCD中,AB=4,取CD中点O,以O为圆心OD为半径作圆交AD于E,交BC的延长线交于点F,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com