
【题目】小明的作业本上有四道利用不等式的性质,将不等式化为x>a或x<a的作业题:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A. 1题 B. 2题
C. 3题 D. 4题
科目:初中数学 来源: 题型:
【题目】边长都为整数的△ABC≌△DEF ,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为( )
A.3
B.4
C.5
D.3或4或5
查看答案和解析>>
科目:初中数学 来源: 题型:
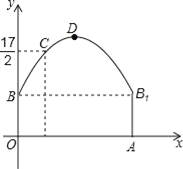
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
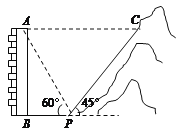
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明。
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E。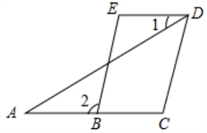
证明:∵BE∥CD (已知 )
∴∠2=∠C ( )
又 ∵∠A=∠1 (已知 )
∴ AC∥DE ( )
∴ ∠2=∠E( )
∴∠C=∠E ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)已知,直线AP是过正方形ABCD顶点A的任一条直线(不过B、C、D三点),点B关于直线AP的对称点为E,连结AE、BE、DE,直线DE交直线AP于点F.
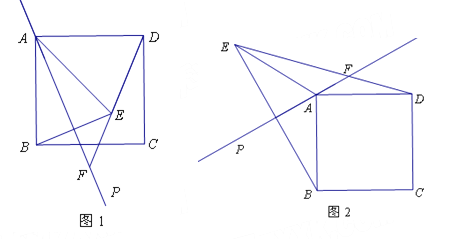
(1)如图1,直线AP与边BC相交.
①若∠PAB=20°,则∠ADF= °,∠BEF= °;
②请用等式表示线段AB、DF、EF之间的数量关系,并说明理由;
(2)如图2,直线AP在正方形ABCD的外部,且![]() ,
,![]() ,求线段AF的长.
,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts. 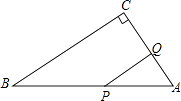
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业2018年初获利润300万元,到2020年初计划利润达到507万元,求这两年的年利润的平均增长率,设企业这两年的年利润平均增长率为x,则可列方程为( )
A. 300(1+x)2=507B. 300(1﹣x)2=507
C. 300(1+2x)=507D. 300(1+x2)=507
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com