
���� ��1����Τ�ﶨ���ɵ�x1+x2=a+1��x1x2=$\frac{1}{4}$a2+1������|x1-x2|=$\sqrt{5}$����x1+x2��2-4x1•x2=5����������a�ķ��̿ɵã�
��2������Τ�ﶨ��֪x1+x2=-p��x1x2=q�����·��������ֱ�Ϊy1��y2����y1=$\frac{1}{{x}_{1}}$��y2=$\frac{1}{{x}_{2}}$����֪y1+y2��y1y2���̶��ɵ��·��̣�
��� �⣺��1���跽��x2-��a+1��x+$\frac{1}{4}$a2+1=0������Ϊx1��x2��
��x1+x2=a+1��x1x2=$\frac{1}{4}$a2+1��
��|x1-x2|=$\sqrt{5}$��
�ࣨx1-x2��2=5������x1+x2��2-4x1•x2=5��
�ࣨa+1��2-4��$\frac{1}{4}$a2+1��=5��
��ã�a=4��
��2������x2+px+q=0��q��0����x1+x2=-p��x1x2=q��
���·��������ֱ�Ϊy1��y2��
��y1=$\frac{1}{{x}_{1}}$��y2=$\frac{1}{{x}_{2}}$��
��y1+y2=$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=-$\frac{p}{q}$��
y1y2=$\frac{1}{{x}_{1}{x}_{2}}$=$\frac{1}{q}$��
���·���Ϊy2+$\frac{p}{q}$y+$\frac{1}{q}$=0��
���� ������Ҫ����һԪ���η��̵ĸ���ϵ���Ĺ�ϵ������ax2+bx+c=0������Ϊx1��x2����x1+x2=-$\frac{b}{a}$��x1•x2=$\frac{c}{a}$��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5��a-b��2 | B�� | 5��b-a��2 | C�� | -��a-b��2 | D�� | ��b-a��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
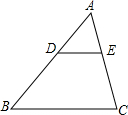 ��ͼ����ABC�У�DE��BC��$\frac{AD}{DB}$=$\frac{1}{2}$��DE=2cm����BC�ߵij��ǣ�������
��ͼ����ABC�У�DE��BC��$\frac{AD}{DB}$=$\frac{1}{2}$��DE=2cm����BC�ߵij��ǣ�������| A�� | 6cm | B�� | 4cm | C�� | 8cm | D�� | 7cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.60��106 | B�� | 1.57��106 | C�� | 1.58��106 | D�� | 1.58��105 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com