
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120,△ABF为等边三角形;点E.F分别在菱形的边BC.CD上滑动,且点E.F不与点B.C.D重合,当点E.F分别在BC.CD上滑动时,求四边形ABCF的面积= ___________并求△CEF面积的最大值___________

【答案】![]()
![]()
【解析】
①连接AC,证明△ABE≌△ACF,将四边形AECF的面积转化为![]() 的面积即可;
的面积即可;
②S△CEF=S四边形AECF﹣S△AEF,![]() 的面积最小,则可得
的面积最小,则可得![]() 的面积最大;当正三角形AEF的边AE与BC垂直时,边AE最短,即
的面积最大;当正三角形AEF的边AE与BC垂直时,边AE最短,即![]() 的面积最小,可得结果.
的面积最小,可得结果.
如图,连接AC,
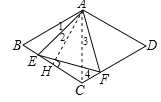
∵四边形ABCD为菱形,
∠BAD=120°,∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,∵∠BAD=120°,∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB.
在△ABE和△ACF中,
∵∠1=∠3,AC=AC,∠ABC=∠4,
∴△ABE≌△ACF(ASA),
∴S△ABE=S△ACF,
∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,
作AH⊥BC于H点,则BH=2,
∴S四边形AECF=S△ABC=![]() BCAH=
BCAH=![]() BC
BC![]() =
=![]() ,
,
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短,
∴△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,
又∵S△CEF=S四边形AECF﹣S△AEF,则此时△CEF的面积就会最大,
∴S△CEF=S四边形AECF﹣S△AEF=![]() ﹣
﹣![]() ×
×![]() ×
×![]() =
=![]() .
.
故答案为![]() .
.



科目:初中数学 来源: 题型:
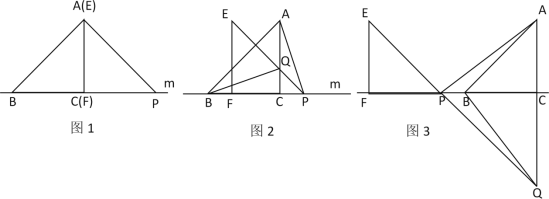
【题目】(1)问题情境,如图1,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△EFP的边FP也在直线m上,边EF与边AC重合,且EF=FP,
在图1中,AB与AP的数量关系是_______,AB与AP的位置关系是_______
(2)操作发现:将△EFP沿直线m向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并证明BQ与AP的数量关系和位置关系
(3)猜想论证:将△EFP沿直线m向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,(2)中的结论还成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
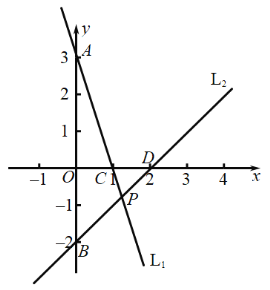
【题目】如图,L1、L2分别表示两个一次函数的图象,它们相交于点P.
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解?
(3)求出图中△APB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应括号里:
![]() ,8.2,-7,0,-0.3,102 ,-2.1010010001…,
,8.2,-7,0,-0.3,102 ,-2.1010010001…,![]() ,
,![]()
非负整数集合:{ …}
分数集合:{ …}
无理数集合:{ …}
负数集合:{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若取前3格子中的任意两个数记作![]() ,且
,且![]() ,那么所有的
,那么所有的![]() 的和可以通过计算
的和可以通过计算![]() 得到,其结果为_____,若
得到,其结果为_____,若![]() 为前
为前![]() 格子中的任意两个数,且
格子中的任意两个数,且![]() ,则所有的
,则所有的![]() 的和为_____.
的和为_____.
9 | ★ | ☆ | x | ﹣6 | 2 | …… |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)6.8-(-4.2)+(-9);
(2)|-2|-(-3)×(-15);
(3)(![]() +
+![]() -
-![]() )×(-24);
)×(-24);
(4)-24÷(![]() )2+3
)2+3![]() ×(-
×(-![]() )-(-0.5)2.
)-(-0.5)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
则下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
C. 二次函数的最小值是![]() D. 抛物线的对称轴是
D. 抛物线的对称轴是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com