
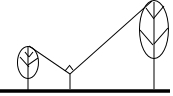
 如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米?
如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米? 分析 过点E作EH⊥AB,EM⊥CD,H、M为垂足,根据相似三角形的判定定理得出△AHE∽△EMC,由相似三角形的对应边成比例求出CM的长,进而可得出结论.
解答 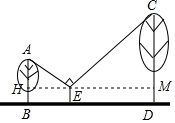 解:过点E作EH⊥AB,EM⊥CD,H、M为垂足,则∠A+∠AEH=90°.
解:过点E作EH⊥AB,EM⊥CD,H、M为垂足,则∠A+∠AEH=90°.
∵∠AEC=90°,
∴∠AEH+∠CEM=90°,
∴∠A=∠CEM.
∵∠AHE=∠CME=90°,
∴△AHE∽△EMC,
∴$\frac{AH}{EM}$=$\frac{HE}{CM}$,即$\frac{4-1.5}{5}$=$\frac{3}{CM}$,解得CM=6,
∴CD=CM+DM=6+1.5=7.5(米).
点评 本题考查的是相似三角形的应用,根据题意作出辅助线,构造出相似三角形是解答此题的关键.


 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
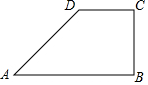 如图,四边形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.
如图,四边形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
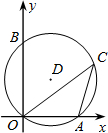 如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com