
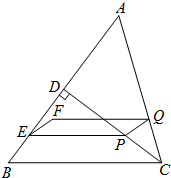
 如图,在△ABC中,AC=BC=5cm,AB=6cm,CD⊥AB于点D.动点P,Q同时从点C出发,点P沿线CD做依次匀速往返运动,回到点C停止;点Q沿折线CA-AD向终点D做匀速运动;点P,Q运动的速度都是5cm/s.过点P作PE∥BC,交AB于点E,连接PQ.当点P,E不重合且点P,Q不重合时,以线段PE,PQ为一组邻边作□PEFQ.设点P运动的时间为t(s),?PEFQ与△ABC重叠部分的面积为S(cm2).
如图,在△ABC中,AC=BC=5cm,AB=6cm,CD⊥AB于点D.动点P,Q同时从点C出发,点P沿线CD做依次匀速往返运动,回到点C停止;点Q沿折线CA-AD向终点D做匀速运动;点P,Q运动的速度都是5cm/s.过点P作PE∥BC,交AB于点E,连接PQ.当点P,E不重合且点P,Q不重合时,以线段PE,PQ为一组邻边作□PEFQ.设点P运动的时间为t(s),?PEFQ与△ABC重叠部分的面积为S(cm2).分析 (1)根据题意,分两种情况:①当0<t<$\frac{4}{5}$时;②当$\frac{4}{5}$<t≤$\frac{8}{5}$时;然后根据PE∥BC,可得$\frac{PE}{BC}$=$\frac{PD}{CD}$,据此用含t的代数式表示线段PE的长即可.
(2)首先用含t的代数式表示出QF、QA,然后根据QA=QF,求出t的值是多少即可.
(3)首先作PM⊥BC于点M,作QN⊥BC于点N,设?PEFQ的高为h,分别用含t的代数式表示出PM、QN,进而用含t的代数式表示出h;然后根据三角形的面积的求法,求出S与t之间的函数关系式即可.
解答 解:(1)∵AC=BC=5cm,CD⊥AB于点D,
∴点D是AB的中点,AD=6÷2=3(cm),
∵AC=5cm,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm).
①当0<t<$\frac{4}{5}$时,如图1,
∵PC=5t,
∴PD=CD-PC=4-5t,
∵PE∥BC,
∴$\frac{PE}{BC}$=$\frac{PD}{DC}$,
∴PE=$\frac{BC•PD}{CD}$=$\frac{5}{4}$PD=$\frac{5}{4}$(4-5t)=5-$\frac{25}{4}$t.
②当$\frac{4}{5}$<t≤$\frac{8}{5}$时,如图2, ,
,
PD=5t-4,
∵PE∥BC,
∴$\frac{PE}{BC}$=$\frac{PD}{DC}$,
∴PE=$\frac{BC•PD}{CD}$=$\frac{5}{4}$PD=$\frac{5}{4}$(5t-4)=$\frac{25}{4}$t-5.
综上所述,PE=$\left\{\begin{array}{l}{5-\frac{25}{4}t}&{(0<t<\frac{4}{5})}\\{\frac{25}{4}t-5}&{(\frac{4}{5}<t≤\frac{8}{5})}\end{array}\right.$.
(2)如图3,
QF=PE=$\frac{25}{4}t$-5,
∵CQ=5t,
∴QA=AC-CQ=5-5t,
∵PE∥BC,PE∥QF,
∴QF∥BC,
∴$\frac{QA}{AC}$=$\frac{QF}{BC}$,
∵AC=BC,
∴QA=QF,
∴5-5t=$\frac{25}{4}$t-5,
解得t=$\frac{8}{9}$.
(3)如图4,作PM⊥BC于点M,作QN⊥BC于点N,
设?PEFQ的高为h,
∵sin∠PCM=$\frac{BD}{BC}$,
∴PM=PC•sin∠PCM=(8-5t)×$\frac{3}{5}$=$\frac{24}{5}$-3t,
∵sin∠QBN=$\frac{CD}{BC}$=$\frac{4}{5}$,
∴QN=BQ•sin∠QBN=[6-(5t-5)]×$\frac{4}{5}$=$\frac{44}{5}$-4t,
∴h=QN-PM=($\frac{44}{5}$-4t)-($\frac{24}{5}$-3t)=4-t,
∴S=$\frac{1}{2}$PE•h=$\frac{1}{2}$($\frac{25}{4}t$-5)×(4-t)=-$\frac{25}{8}$t2+15t-10.
点评 本题考查了相似形综合题、函数关系式的求法、矩形的性质和应用、三角函数的应用、三角形的面积的求法等知识,解题的关键是学会分类讨论思想的应用,需要一定的分析推理能力,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
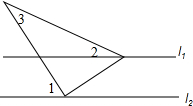 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )| A. | 27°20′ | B. | 26°40′ | C. | 27°40′ | D. | 73°20′ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.8 | B. | 9.6 | C. | 9.5 | D. | 9.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
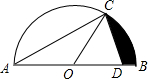 如图,AB是半圆O的直径,点C在半圆上,点D在AB上,且AC=AD,OC=2,∠CAB=30°.
如图,AB是半圆O的直径,点C在半圆上,点D在AB上,且AC=AD,OC=2,∠CAB=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com