
分析 正方形的边长与对角线的比=sin45°=$\frac{\sqrt{2}}{2}$,即可得出结果;等边三角形的高与边长的比=sin60°=$\frac{\sqrt{3}}{2}$,即可得出结果.
解答 解:如图1所示: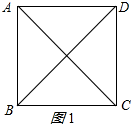 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,AC=BD,∠BAD=90°,
∴∠ABD=45°,
∴AB:BD=sin45°=$\sqrt{2}$:2;
故答案为:$\sqrt{2}$:2;
如图2所示:∵△EFG是等边三角形,EH是高,
∴EF=FG=GE,∠EFH=60°,∠EHF=90°,
∴sin60°=$\frac{EH}{EF}$=$\frac{\sqrt{3}}{2}$,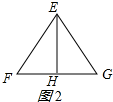
∴EF:EH=2:$\sqrt{3}$;
故答案为:2:$\sqrt{3}$.
点评 本题考查了正方形的性质、等边三角形的性质、三角函数的运用;熟练掌握正方形和等边三角形的性质,运用三角函数进行计算是解决问题的关键.


科目:初中数学 来源: 题型:选择题
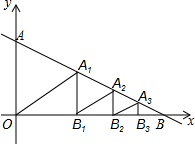 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{4}^{n-1}}$ | D. | $\frac{1}{{4}^{n}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
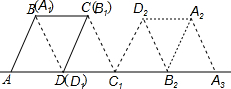 如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.
如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:填空题
如下图所示,有一电路AB是由图示的开关控制,任意地闭合两个开关,使电路形成通路. 能使电路形成通路的概率为____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com