
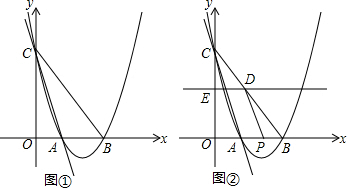
分析 (1)先由直线的解析式求得点A和点C的坐标,然后由AB=2,可求得点B的坐标,设抛物线的解析式为y=a(x-1)(x-3),将C(0,4)代入求得a的值即可;
(2)首先证明△CDE∽△COB,依据相似三角形的性质可求得DE的长(用含t的式子表示),然后依据S△EDP=$\frac{1}{2}$DE•OE列出△EDP的面积与t的函数关系式即可;(3)过点D作DM⊥x轴,垂足为M,由AP=AB-PB可得到AP的长,由可知D(3-$\frac{3}{2}$t),然后可求得AM,PM的长,依据勾股定理可求得AD、DP的长,然后依据分为AD=PD、AD=AP、AP=PD三种情况列方程求解即可.
解答 解:(1)将x=0代入y=-4x+4,得:y=4,
∴C(0,4).
将y=0代入y=-4x+4得:-4x+4=0,解得x=1,
∴A(1,0).
∵AB=2,
∴B(3,0).
设抛物线的解析式为y=a(x-1)(x-3),将C(0,4)代入得:3a=4,解得:a=$\frac{4}{3}$,
∴抛物线的解析式为y=$\frac{4}{3}$x2-$\frac{16}{3}$x+4.
(2)由题意得:OE=2t,BP=t.
∵C(0,4),B(3,0),
∴OC=4,OB=3.
∴CE=4-2t,OP=3-t.
∵ED∥OB,
∴△CDE∽△COB.
∴$\frac{DE}{OB}$=$\frac{CE}{OC}$,
∴$\frac{DE}{3}$=$\frac{4-2t}{4}$.
∴DE=3-$\frac{3}{2}$t.
∴S△EDP=$\frac{1}{2}$DE•OE=$\frac{1}{2}$×$\frac{6-3t}{2}$×2t=-$\frac{3}{2}$t2+3t=-$\frac{3}{2}$(t-1)2+$\frac{3}{2}$.
∴当t=1时,△EDP面积最大值为$\frac{3}{2}$.
∴OP=3-t=3-1=2.
(3)如图所示:过点D作DM⊥x轴,垂足为M.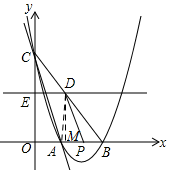
∵AP=AB-PB=2-t,
∴AP2=(2-t)2.
由勾股定理可知:AD2=AM2+MD2=(2-$\frac{3}{2}$t)2+(2t)2,PD2=PM2+DM2=($\frac{1}{2}$t)2+(2t)2.
当AD=PD时,AD2=PD2,(2-$\frac{3}{2}$t)2+(2t)2=($\frac{1}{2}$t)2+(2t)2,解得:t=1,t=2(舍去);
当AD=AP时,AD2=AP2,(2-$\frac{3}{2}$t)2+(2t)2=(2-t)2,解得:t=$\frac{8}{21}$,t=0(舍去).
当AP=PD时,AP2=PD2,(2-t)2=($\frac{1}{2}$t)2+(2t)2,解得:t=$\frac{4\sqrt{17}-8}{13}$,t=$\frac{-4\sqrt{17}-8}{13}$(舍去).
综上所述,当t=1或t=$\frac{8}{21}$或t=$\frac{4\sqrt{17}-8}{13}$时,△ADP为等腰三角形.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的性质、待定系数法求二次函数的解析式、等腰三角形的定义、勾股定理,依据题意列出△EDP的面积与t的函数关系式是解答问题(2)的关键,用含t的式子表示AD、PD、AP的长是解答问题(3)的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
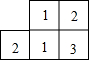 如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图.
如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com