
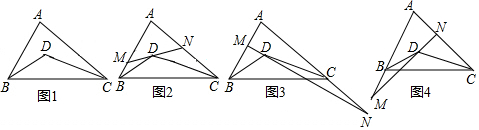
分析 (1)由∠MDB+∠NDC+∠BDC=180°结合∠BDC=90°+$\frac{1}{2}$∠A,即可求出∠MDB+∠NDC=90°-$\frac{1}{2}$∠A;
(2)由∠MDB+∠BDC-∠NDC=180°结合∠BDC=90°+$\frac{1}{2}$∠A,即可得出∠MDB-∠NDC=90°-$\frac{1}{2}$∠A;
(3)由∠BDC-∠BDM+∠NDC=180°结合∠BDC=90°+$\frac{1}{2}$∠A,即可得出∠NDC-∠BDM=90°-$\frac{1}{2}$∠A.
解答 解:(1)∵∠MDB+∠NDC+∠BDC=180°,
∴∠MDB+∠NDC=180°-∠BDC.
∵∠BDC=90°+$\frac{1}{2}$∠A,
∴∠MDB+∠NDC=180°-(90°+$\frac{1}{2}$∠A)=90°-$\frac{1}{2}$∠A.
(2)∠MDB-∠NDC=90°-$\frac{1}{2}$∠A,理由如下:
∵∠MDB+∠BDN=180°,∠BDN=∠BDC-∠NDC,
∴∠MDB+∠BDC-∠NDC=180°.
∵∠BDC=90°+$\frac{1}{2}$∠A,
∴∠MDB+90°+$\frac{1}{2}$∠A-∠NDC=180°,
∴∠MDB-∠NDC=90°-$\frac{1}{2}$∠A.
(3)∠NDC-∠BDM=90°-$\frac{1}{2}$∠A,理由如下:
∵∠MDC+∠NDC=180°,∠BDC=∠BDM+∠MDC,
∴∠BDC-∠BDM+∠NDC=180°.
∵∠BDC=90°+$\frac{1}{2}$∠A,
∴90°+$\frac{1}{2}$∠A-∠BDM+∠NDC=180°,
∴∠NDC-∠BDM=90°-$\frac{1}{2}$∠A.
点评 本题考查了三角形内角和定义以及角的计算,解题的关键是:(1)根据角与角之间的关系找出∠MDB+∠NDC+∠BDC=180°;(2)根据角与角之间的关系找出∠MDB+∠BDC-∠NDC=180°;(3)根据角与角之间的关系找出∠BDC-∠BDM+∠NDC=180°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
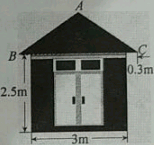 一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
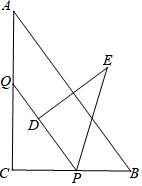 如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 45元 | B. | 14元 | C. | 45元或14元 | D. | 50元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com