
分析 先将两个方程的解用含m的代数式表示出来,再根据方程$\frac{13m+x}{2}$=4的解是$\frac{2x-3m}{3}$-$\frac{x-1}{4}$=$\frac{1}{6}$x-1的解的5倍,列出关于m的方程进行求解即可.
解答 解:∵$\frac{13m+x}{2}$=4
13m+x=8
∴x=8-13m,
∵$\frac{2x-3m}{3}$-$\frac{x-1}{4}$=$\frac{1}{6}$x-1
4(2x-3m)-3(x-1)=2x-12
8x-12m-3x+3=2x-12
3x=12m-15
∴x=4m-5,
∵方程$\frac{13m+x}{2}$=4的解是$\frac{2x-3m}{3}$-$\frac{x-1}{4}$=$\frac{1}{6}$x-1的解的5倍,
∴8-13m=5(4m-5),
解得m=1.
点评 本题主要考查了解一元一次方程和一元一次方程的解,解题时注意:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.把方程的解代入原方程,等式左右两边相等.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
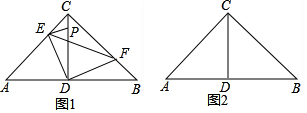
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
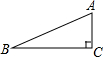 (1)如图,△ABC中,∠C=90°,那么:①∠A+∠B=90°;②tanA•tanB的值为1;
(1)如图,△ABC中,∠C=90°,那么:①∠A+∠B=90°;②tanA•tanB的值为1;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com