
分析 把m看做已知数表示出方程组的解,根据方程组的解都大于1,求出m的范围即可.
解答 解:$\left\{\begin{array}{l}{3x-4y=m①}\\{x+2y=2m+3②}\end{array}\right.$,
①+②×2,得
5x=5m+6,
解得,x=m+1.2,
把x=m+1.2代入②,得
y=$\frac{1}{2}$m+0.9,
∵关于x、y的二元一次方程组$\left\{\begin{array}{l}{3x-4y=m}\\{x+2y=2m+3}\end{array}\right.$的解都大于1,
∴$\left\{\begin{array}{l}{m+1.2>1}\\{\frac{1}{2}m+0.9>1}\end{array}\right.$,
解得,m>0.2,
即m的取值范围是m>0.2.
点评 此题考查了二元一次方程组的解,解答本题的关键是明确方程组的解即为能使方程组中两方程都成立的未知数的值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
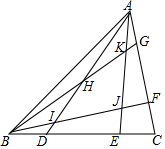 如图,在△ABC中,BC边上依次有B、D、E、C,AC边上依次有A、G、F,满足BD=CE=$\frac{1}{4}$BC,CF=AG=$\frac{1}{4}$AC,BF交AE于点J,交AD于I,BG交AE于点K,交AD于点H,且S△ABC=1,求S四边形KHIJ.
如图,在△ABC中,BC边上依次有B、D、E、C,AC边上依次有A、G、F,满足BD=CE=$\frac{1}{4}$BC,CF=AG=$\frac{1}{4}$AC,BF交AE于点J,交AD于I,BG交AE于点K,交AD于点H,且S△ABC=1,求S四边形KHIJ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com