已知某易拉罐厂设计一种易拉罐，在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系：
| 底面半径x（cm） | 1.6 | 2.0 | 2.4 | 2.8 | 3.2 | 3.6 | 4.0 |
| 用铝量y（cm | 6.9 | 6.0 | 5.6 | 5.5 | 5.7 | 6.0 | 6.5 |
（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）当易拉罐底面半径为2.4cm时，易拉罐需要的用铝量是多少？
（3）根据表格中的数据，你认为易拉罐的底面半径为多少时比较适宜？说说你的理由．
（4）粗略说一说易拉罐底面半径对所需铝质量的影响．
科目：初中数学 来源： 题型：
为了提高新产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场。现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两间工厂了解情况，获得如下信息：
信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍。
根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品？
查看答案和解析>>
科目：初中数学 来源： 题型：
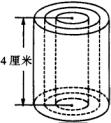
如图所示，圆柱的高是4厘米，当圆柱底面半径r（厘米）变化时，圆柱的体积V（厘米
）也随之变化．
（1）在这个变化过程中，自变量是______，因变量是____．
（2）圆柱的体积V与底面半径r的关系式是____．
（3）当圆柱的底面半径由2变化到8时，圆柱的体积由____变化到____．
查看答案和解析>>
科目：初中数学 来源： 题型：
已知△ABC的底边BC上的高为8cm，当它的底边BC从16cm变化到5cm时，△ABC的面积（ ）
（A）从20cm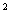
变化到64cm 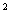（B）从64c
m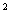变化到20cm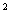
（C）从128cm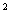变化到40cm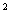（D）从40cm变化到128cm
查看答案和解析>>
科目：初中数学 来源： 题型：
甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们
离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系的图象如图所示，根据图中提供的信息，有下列说法：( )
（1） 他们都行驶了18千米；
（2） 甲在途中停留了0.5小时；
（3） 乙比甲晚出发了0.5小时；
（4） 相遇后，甲的速度小于乙的速度；
（5） 甲、乙两人同时到达目的地。
其中，符合图象描述的说法有
A.2个 B.4个 C.3个 D.5个
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
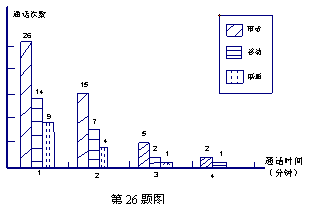
下面的统计图反映了某中国移动用户5月份手机的使用情况，该用户的通话对象分为三类：市内电话，本地中国移动用户，本地中国联通用户．
（1）该用户5月份通话的总次数为 次．
（2）已知该用户手机的通话均按0.6元/分钟计费，求该用户5月份的话费（通话时间不满1分钟按1分钟计算。例如，某次实际通话时间为1分23秒，按通话时间2分钟计费，话费为1.2元）；
（3）当地中国移动公司推出了名为“越打越便宜”的优惠业务，优惠方式为：若与其它中国移动用户通话，第1分钟为0.4元，第2分钟为0.3元。第3分钟起就降为每分钟0.2元，每月另收取基本费10元，其余通话计费方式不变。如果使用了该业务，则该用户5月份的话费会是多少？
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的解是 ；
，的整数解仅有1，2，那么适合这个不等式组的整数a，b组成的有序数对[a，b]共有 个。