练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．解方程：$\frac{2}{2-x}$+x=$\frac{{x}^{2}}{x-2}$．

    分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

    解答 解：去分母得：-2+x2-2x=x2，
    解得：x=-1，
    经检验x=-1是分式方程的解．

    点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

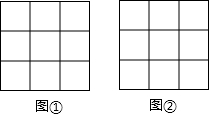    20．在边长为1个单位长度的小正方形组成的3×3的正方形网格图①、图②中，各画一个顶点在格点上的平行四边形，要求：每个平行四边形均为轴对称图形，每个平行四边形至少有一条边长为$\sqrt{5}$，所画的两个四边形不全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．解方程：（1）（2x+1）（x+2）=3；
                  （2）（x-2）2+4x（x-2）=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．【阅读材料，获取新知】
    善于思考的小军在解方程组
    $\left\{\begin{array}{l}{2x+5y=3（1）}\\{4x+11y=5（2）}\end{array}\right.$时，采用了一种“整体代换法”的解法．
    解：将方程（2）变形：4x+10y+y=5即2（2x+5y）+y=5（3）
    把方程（1）代入（3）得：2×3+y=5
    ∴y=-1．
    把y=-1，代入（1）得x=4
    ∴方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$
    【利用新知，解答问题】
    请你利用小军的“整体代换法”解决一下问题：
    （1）解方程组：
    ①$\left\{\begin{array}{l}{3x-2y=5}\\{9x-4y=19}\end{array}\right.$                   ②$\left\{\begin{array}{l}{2x-3y-2=0}\\{\frac{2x-3y+5}{7}+2y=9}\end{array}\right.$
    （2）已知x，y满足方程组$\left\{\begin{array}{l}{{3x}^{2}-2xy+1{2y}^{2}=47}\\{{2x}^{2}+xy+{8y}^{2}=36}\end{array}\right.$，则x2+4y2与xy的值分别为17、2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

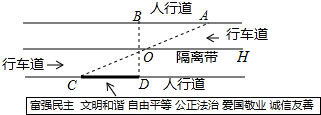    5．杨阳同学沿一段笔直的人行道行走，在由A处步行到达B处的过程中，通过隔离带的空隙O，刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD，创设数学情境如下：
    如图，AB∥OH∥CD，相邻两平行线间的距离相等，AC，BD相交于点O，OD⊥CD，垂足为D，已知AB=20米，根据上述信息杨阳同学求出了标语CD的长度．（请将杨阳同学的解答过程补充完整）
    解：因为AB∥DC，
    所以∠ABO=∠CDO（依据是两直线平行，内错角相等）
    又因为DO⊥CD，
    所以∠CDO=90°，
    所以∠ABO=90°，
    所以BO⊥AB．
    因为相邻两平行线间的距离相等，
    所以BO=DO．
    在△BOA和△DOC中，
    ∠ABO=∠CDO，
    BO=DO，
    ∠AOB=∠COD，（依据是对顶角相等）
    所以△BOA≌△DOC（ASA）．
    所以CD=AB=20米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某校在设立学生奖学金时规定：综合成绩最高分获得一等奖、综合成绩包括智育成绩、德育成绩、体育成绩三项，这三项成绩分别按60%、30%、10%的比例计入综合成绩．现有小天、小颖两位同学入选奖学金一等奖的评选，他们的智育成绩、德育成绩、体育成绩如表，请通过计算判断谁能拿到一等奖．
    学生体育成绩德育成绩学习成绩
    小天88分84分90分
    小颖90分85分88分

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图是一个5×5的正方形网格，每个小正方形的边长都是1，请在此网格中画出一个顶点都在格点且面积为17的正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．一个不透明的布袋里装有7个只有颜色不同的球，其中4个红球、3个白球，从布袋中随机摸出一个球，则摸到红球的概率是$\frac{4}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

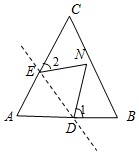    20．如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别在边AB、AC上，将△ABC沿着DE折叠压平，使点A与点N重合．
    （1）若∠B=35°，∠C=60°，求∠A的度数；
    （2）若∠A=70°，求∠1+∠2的度数．

    查看答案和解析>>

    同步练习册答案