
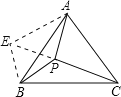
【题目】如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
(1)在图中画出:将△BPC绕点B逆时针旋转60°后得到△BEA;
(2)连接EP,完成你的解答.

【答案】(1)详见解析;(2)150°.
【解析】
(1)将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质画出图形即可;(2)连EP,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数.
(1)如图:将△BPC绕点B逆时针旋转60°得△BEA;
(2) 连EP,
∴BE=BP=4,AE=PC=5,PBE=60°
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=
(k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=![]() ,点B的坐标(6,n).
,点B的坐标(6,n).
(1)求反比例函数和一次函数的解析式.
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形OABC放在平面直角坐标系中,O为原点,点A在x轴的正半轴上,B(8,6),点D是射线AO上的一点,把△BAD沿直线BD折叠,点A的对应点为A′.
(Ⅰ)若点A′落在矩形的对角线OB上时,OA′的长= ;
(Ⅱ)若点A′落在边AB的垂直平分线上时,求点D的坐标;
(Ⅲ)若点A′落在边AO的垂直平分线上时,求点D的坐标(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是![]() .”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
.”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是______事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每6个人中会有1人抽中一等奖、2人抽中二等奖,若袋中共有18个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中增加3个黄球,那么抽中一等奖的概率会怎样变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=1,AD=![]() ,BD=2,∠ABC+∠ADC=180°,CD=
,BD=2,∠ABC+∠ADC=180°,CD=![]() .
.
(1)判断△ABD的形状,并说明理由;
(2)求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.
若只在国内销售,销售价格![]() (元/件)与月销量
(元/件)与月销量![]() (件)的函数关系式为
(件)的函数关系式为![]() ,成本为
,成本为![]() 元/件,无论销售多少,每月还需支出广告费
元/件,无论销售多少,每月还需支出广告费![]() 元,设月利润为
元,设月利润为![]() (元).
(元).
若只在国外销售,销售价格为![]() 元/件,受各种不确定因素影响,成本为
元/件,受各种不确定因素影响,成本为![]() 元/件
元/件![]() 为常数,
为常数,![]() ,当月销量为
,当月销量为![]() (件)时,每月还需缴纳
(件)时,每月还需缴纳![]() 元的附加费,设月利润为
元的附加费,设月利润为![]() (元).
(元).
![]() 当
当![]() 时,
时,![]() ________元/件;
________元/件;
![]() 分别求出
分别求出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如果某月要求将
如果某月要求将![]() 件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售,才能使所获月利润较大?
件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售,才能使所获月利润较大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com