
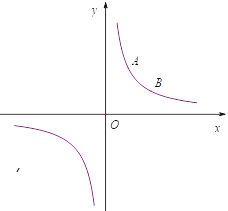
【题目】如图所示,已知![]() 点的横坐标为2,将
点的横坐标为2,将![]() 点向右平移2个单位,再向下平移2个单位得到
点向右平移2个单位,再向下平移2个单位得到![]() 点,且
点,且![]() 、
、![]() 两点均在双曲线
两点均在双曲线![]() 上.
上.
(1)求反比例函数的解析式.(2)若直线![]() 于反比例函数
于反比例函数![]() 的另一交点为
的另一交点为![]() ,求
,求![]() 的面积.
的面积.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线L:![]() 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为
经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为![]() .
.
(1)求抛物线L的表达式;
(2)点P在抛物线![]() 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考
(1)“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线;C1:y=﹣![]() (x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.

(1)求点B、点C的坐标;
(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲜丰水果店计划用![]() 元/盒的进价购进一款水果礼盒以备销售.
元/盒的进价购进一款水果礼盒以备销售.
![]() 据调查,当该种水果礼盒的售价为
据调查,当该种水果礼盒的售价为![]() 元/盒时,月销量为
元/盒时,月销量为![]() 盒,每盒售价每增长
盒,每盒售价每增长![]() 元,月销量就相应减少
元,月销量就相应减少![]() 盒,若使水果礼盒的月销量不低于
盒,若使水果礼盒的月销量不低于![]() 盒,每盒售价应不高于多少元?
盒,每盒售价应不高于多少元?
![]() 在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了
在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了![]() ,而每盒水果礼盒的售价比(1)中最高售价减少了
,而每盒水果礼盒的售价比(1)中最高售价减少了![]() ,月销量比(1)中最低月销量
,月销量比(1)中最低月销量![]() 盒增加了
盒增加了![]() ,结果该月水果店销售该水果礼盒的利润达到了
,结果该月水果店销售该水果礼盒的利润达到了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由点P(14,1),A(![]() ,0),B(0,
,0),B(0,![]() )(
)(![]() ),确定的△PAB的面积为18,则
),确定的△PAB的面积为18,则![]() 的值为_________,如果
的值为_________,如果![]() ,则
,则![]() 的值为_____________________
的值为_____________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.
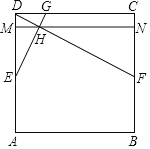
(1)猜想![]() 与
与![]() 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;
(2)过点![]() 作
作![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,若正方形
,若正方形![]() 的边长为10,点
的边长为10,点![]() 是
是![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面上A、B两点,给出如下定义:以点A为中心,B为其中一个顶点的正方形称为点A、B的“领域”.
(1)已知点A的坐标为(﹣1,1),点B的坐标为(3,3),顶点A、B的“领域”的面积为 .
(2)若点A、B的“领域”的正方形的边与坐标轴平行或垂直,回答下列问题:
①已知点A的坐标为(2,0),若点A、B的“领域”的面积为16,点B在x轴上方,求B点坐标;
②已知点A的坐标为(2,m),若在直线l:y=﹣3x+2上存在点B,点A、B的“领域”的面积不超过16,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
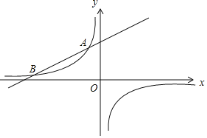
【题目】如图,反比例函数y=![]() 与一次函数y=ax+b的图象交于点A(﹣2,6)、点B(n,1).
与一次函数y=ax+b的图象交于点A(﹣2,6)、点B(n,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com