
【题目】在![]() ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
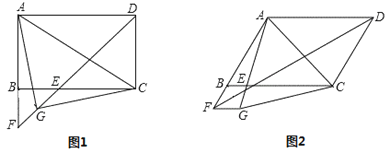
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,判断△AGC的形状.(直接写出结论不必证明)
【答案】(1)①证明见解析;②△AGC是等腰直角三角形.证明见解析;(2)△AGC是等边三角形.
【解析】试题分析:(1)①先判定四边形ABCD是矩形,再根据矩形的性质可得∠ABC=90°,AB∥DC,AD∥BC,然后根据平行线的性质求出∠F=∠FDC,∠BEF=∠ADF,再根据DF是∠ADC的平分线,利用角平分线的定义得到∠ADF=∠FDC,从而得到∠F=∠BEF,然后根据等角对等边的性质即可证明;
②连接BG,根据等腰直角三角形的性质可得∠F=∠BEF=45°,再根据等腰三角形三线合一的性质求出BG=FG,∠F=∠CBG=45°,然后利用“边角边”证明△AFG和△CBG全等,根据全等三角形对应边相等可得AG=CG,再求出∠GAC+∠ACG=90°,然后求出∠AGC=90°,然后根据等腰直角三角形的定义判断即可;
(2)连接BG,根据旋转的性质可得△BFG是等边三角形,再根据角平分线的定义以及平行线的性质求出AF=AD,平行四边形的对角相等求出∠ABC=∠ADC=60°,然后求出∠CBG=60°,从而得到∠AFG=∠CBG,然后利用“边角边”证明△AFG和△CBG全等,根据全等三角形对应边相等可得AG=CG,全等三角形对应角相等可得∠FAG=∠BCG,然后求出∠GAC+∠ACG=120°,再求出∠AGC=60°,然后根据等边三角形的判定方法判定即可.
试题解析:(1)证明:①∵四边形ABCD是平行四边形,∠ADC=90°,
∴四边形ABCD是矩形,∴∠ABC=90°,AB∥DC,AD∥BC,
∴∠F=∠FDC,∠BEF=∠ADF,
∵DF是∠ADC的平分线,∴∠ADF=∠FDC,∴∠F=∠BEF,
∴BF=BE;
②△AGC是等腰直角三角形.
理由如下:连接BG,
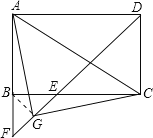
由①知,BF=BE,∠FBC=90°,∴∠F=∠BEF=45°,
∵G是EF的中点,∴BG=FG,∠F=∠CBG=45°,
∵∠FAD=90°,∴AF=AD,又∵AD=BC,∴AF=BC,
在△AFG和△CBG中, 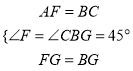 ∴△AFG≌△CBG,
∴△AFG≌△CBG,
∴AG=CG,∠FAG=∠BCG,
又∵∠FAG+∠GAC+∠ACB=90°,∴∠BCG+∠GAC+∠ACB=90°,
即∠GAC+∠ACG=90°,∴∠AGC=90°,∴△AGC是等腰直角三角形;
(2)△AGC是等边三角形.
证明:连接BG,∵FB绕点F顺时针旋转60°至FG,
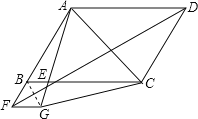
∴△BFG是等边三角形,
∴FG=BG,∠FBG=60°,
又∵四边形ABCD是平行四边形,∠ADC=60°,
∴∠ABC=∠ADC=60°
∴∠CBG=180°-∠FBG-∠ABC=180°-60°-60°=60°,
∴∠AFG=∠CBG,
∵DF是∠ADC的平分线,
∴∠ADF=∠FDC,
∵AB∥DC,
∴∠AFD=∠FDC,
∴∠AFD=∠ADF,
∴AF=AD,
在△AFG和△CBG中,
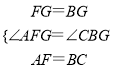 ,
,
∴△AFG≌△CBG(SAS),
∴AG=CG,∠FAG=∠BCG,
在△ABC中,∠GAC+∠ACG=∠ACB+∠BCG+∠GAC=∠ACB+∠BAG+∠GAC=∠ACB+∠BAC=180°-60°=120°,
∴∠AGC=180°-(∠GAC+∠ACG)=180°-120°=60°,
∴△AGC是等边三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2016年5月某日,重庆部分区县的最高温度如下表所示:
地区 | 合川 | 永川 | 江津 | 涪陵 | 丰都 | 梁平 | 云阳 | 黔江 |
温度(℃) | 25 | 26 | 29 | 26 | 24 | 28 | 28 | 29 |
则这组数据的中位数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过_____次移动后该点到原点的距离为2018个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为( ) 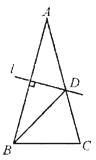
A.50°
B.30°
C.75°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A、B、C三点对应的数分别是a、b、c,若ab<0,c为最大的负整数,c>a且|b|>|a|.
(1)请在数轴上标出A,B,C三点的大致位置;
(2)化简|a﹣b|+|b﹣a+c|﹣|b﹣c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式2x3y﹣xy+16的次数为a,常数项为b,a,b分别对应着数轴上的A、B两点.
(1)a= ,b= ;并在数轴上画出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商店将A品牌彩电按成本价提高50%,然后在广告上写“大酬宾,八折优惠”,结果每台A品牌彩电仍获利300元,则每台A品牌彩电的成本价是_____元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com