
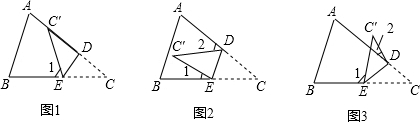
分析 (1)根据外角定理和折叠性质可得结论;
(2)由三角形内角和得:∠EDC+∠DEC=180°-∠C,由折叠得:∠DEC′+∠EDC′=180°-∠C,根据平角定义,得∠1+∠DEC+∠DEC′=180°,∠2+∠EDC+∠EDC′=180°,代入可得:∠1+∠2=2∠C;
(3)根据三角形的内角和得:∠C′ED=180°-∠C′-∠2-∠EDM,由折叠得:∠C′ED=∠DEC,∠C=∠C′,则2∠C′ED=360°-2∠C′-2∠2-2∠EDM,由平角定义得:∠1+∠C′ED+∠DEC=180°,等量代换可得出结论.
解答 解:(1)∠1=2∠C,理由是:
如图1,由折叠得:∠C=∠EC′C,
∵∠1是△EC′C的一个外角,
∴∠1=∠C+∠EC′C,
∴∠1=2∠C;
(2)∠1+∠2=2∠C,理由是:
如图2,∵∠EDC+∠DEC+∠C=180°,
∴∠EDC+∠DEC=180°-∠C,
由折叠得:∠EDC=∠EDC′,∠DEC=∠DEC′,
∵∠1+∠DEC+∠DEC′=180°,
∠2+∠EDC+∠EDC′=180°,
∴∠1+∠2=360°-(∠DEC+∠DEC′+∠EDC+∠EDC′)=360°-2(180°-∠C)=2∠C;
(3)∠1-∠2=2∠C,理由是:
如图3,延长C′D,交BC于F,
在△EDC′中,∠C′ED+∠EDC′+∠C′=180°,
即∠C′ED=180°-∠C′-∠2-∠EDM,
由折叠得:∠C′ED=∠DEC,∠C=∠C′,
∴∠C′ED+∠DEC=2∠C′ED=360°-2∠C′-2∠2-2∠EDM,
∵∠1+∠C′ED+∠DEC=180°,
∴∠1+360°-2∠C′-2∠2-2∠EDM=180°,
∵∠EDM=∠EDF,
∴2∠EDM=180°-∠2,
∴∠1+360°-2∠C-2∠2-(180°-∠2)=180°,
∠1-∠2=2∠C.
点评 本题考查了翻折变换中的折叠问题,明确折叠前后的两个角相等,本题还考查了三角形的内角和定理、外角定理、平角定义等有关于角的性质,根据角的等式之间的化简得出相应的结论.


科目:初中数学 来源: 题型:解答题
| 楼 层 | 一 | 二 | 三 | 四 | 五 | 六 |
| 差价百分比 | 0% | +8% | +17% | +16% | +2% | -10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
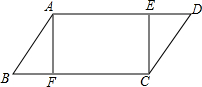 如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:
如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
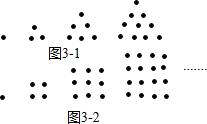 古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:
古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
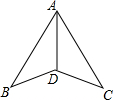 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )| A. | AB=AC,BD=CD | B. | ∠B=∠C,BD=CD | C. | ∠B=∠C,∠BAD=∠CA | D. | ∠ADB=∠ADC,DB=DC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com