

 ,PA=
,PA= AH,求BD的长;
AH,求BD的长;
 ,∴可设AH=3k,则DH=4k,
,∴可设AH=3k,则DH=4k, AH,∴PA=(
AH,∴PA=( )k,
)k,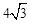 k。
k。 。∴∠P=30°,∠PDH=60°。
。∴∠P=30°,∠PDH=60°。 。
。 ﹣4k,∴HC=
﹣4k,∴HC=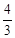 (
( ﹣4k)。
﹣4k)。 。
。 。
。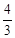 (
( ﹣4k)=
﹣4k)= +7,
+7, BD•AC=
BD•AC= ×
× ×(
×( +7)=900+
+7)=900+ 。
。 ,可设AH=3k,则DH=4k,又由PA=
,可设AH=3k,则DH=4k,又由PA= AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE•cos30°=
AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE•cos30°= 。
。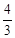 (
( ﹣4k),又由PD2=PA×PC,可得方程:
﹣4k),又由PD2=PA×PC,可得方程: ,解此方程即可求得AC的长,继而求得四边形ABCD的面积。
,解此方程即可求得AC的长,继而求得四边形ABCD的面积。

科目:初中数学 来源:不详 题型:单选题
 的中点,则下列结论不成立的是( )
的中点,则下列结论不成立的是( )
| A.OC//AE | B.EC=BC | C.∠DAE=∠ABE | D.AC⊥OE |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com