
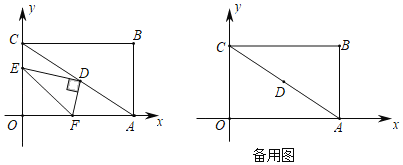
【题目】如图,在平面直角坐标系中,矩形OABC边OA,OC分别在x轴,y的正半轴上,且OA=8,OC=6,连接AC,点D为AC中点,点E从点C出发以每秒1个单位长度运动到点O停止,设运动时间为t秒(0<t<6),连接DE,作DF⊥DE交OA于点F,连接EF.
(1)当t的值为 时,四边形DEOF是矩形;
(2)用含t的代数式表示线段OF的长度,并说明理由;
(3)当△OEF面积为![]() 时,请直接写出直线DE的解析式.
时,请直接写出直线DE的解析式.
【答案】(1)3;(2)![]() +
+![]() t;(3)y=﹣
t;(3)y=﹣![]() x+4或y=﹣
x+4或y=﹣![]() x+
x+![]() .
.
【解析】
(1)根据DE⊥OC得到DE∥OA,由线段的中点的定义得到CD=AD,从而可得到结论;
(2)如图所示:作DM⊥OA于M,DN⊥OC于N,推出四边形DMON是矩形,求得DM=![]() OC=3,DN=
OC=3,DN=![]() OA=4,根据相似三角形的性质得到FM=
OA=4,根据相似三角形的性质得到FM=![]() EN,于是得到结论;
EN,于是得到结论;
(3)由OA=8,OC=6,得到A(8,0),C(0,6),求得D(4,3),根据三角形的面积列方程得到t=2或![]() ,从而可得到直线DE的解析式.
,从而可得到直线DE的解析式.
(1)根据平行线的判定定理得到DE∥OA,由线段的中点的定义得到CD=AD,于是得到结论,
(2)如图所示:作DM⊥OA于M,DN⊥OC于N,推出四边形DMON是矩形,求得DM=![]() OC=3,DN=
OC=3,DN=![]() OA=4,根据相似三角形的性质得到FM=
OA=4,根据相似三角形的性质得到FM=![]() EN,于是得到结论;
EN,于是得到结论;
(3)由OA=8,OC=6,得到A(8,0),C(0,6),求得D(4,3),根据三角形的面积列方程得到t=2或![]() ,于是得到结论.
,于是得到结论.
【解答】
解:(1)当DE⊥OC时,四边形DEOF是矩形;
∵DE⊥OC,
∴DE∥OA,
∵点D为AC中点,
∴CD=AD,
∴CE=OE=![]() OC=3,
OC=3,
∴t=3,
∴当t的值为3s时,四边形DEOF是矩形,
故答案为:3;
(2)如图所示:作DM⊥OA于M,DN⊥OC于N,
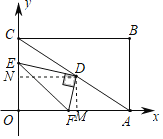
∵四边形OABC是矩形,
∴OA⊥OC,
∴四边形DMON是矩形,
∴∠MDN=90°,DM∥OC,DN∥OA,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∵点D为OB的中点,
∴M、N分别是OA、AB的中点,
∴DM=![]() OC=3,DN=
OC=3,DN=![]() OA=4,
OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN,
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE,
∴![]() =
=![]() =
=![]() ,
,
∴FM=![]() EN,
EN,
∵CN=![]() OC=3,CE=t,
OC=3,CE=t,
∴EN=3﹣t,
∴FM=![]() EN=
EN=![]() ﹣
﹣![]() t,
t,
∴OF=4﹣FM=![]() +
+![]() t;
t;
(3)∵OA=8,OC=6,
∴A(8,0),C(0,6),
∵点D为AC中点,
∴D(4,3),
∵CE=t,
∴OE=6﹣t,
∵OF=![]() +
+![]() t,
t,
∴△OEF面积=![]() OEOF=
OEOF=![]() (6﹣t)(
(6﹣t)(![]() +
+![]() t)=
t)=![]() ,
,
解得:t=2或![]() ,
,
当t=2时,点E(0,4),
∴直线DE的解析式为y=﹣![]() x+4;
x+4;
当t=![]() 时,点E(0,
时,点E(0,![]() ),
),
∴直线DE的解析式为y=﹣![]() x+
x+![]() ,
,
综上所述,直线DE的解析式为y=﹣![]() x+4或y=﹣
x+4或y=﹣![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
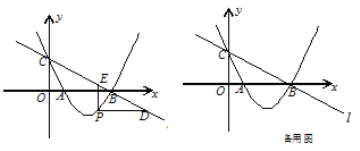
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=![]() (即tan∠DEM=
(即tan∠DEM=![]() ),且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上,求条幅AB的长度(结果保留根号).
),且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上,求条幅AB的长度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
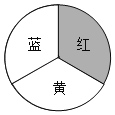
【题目】某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖(若指针恰好停在分割线上则重转).
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品.
(1)若选择方案一,则可领取一份奖品的概率是 ;
(2)选择哪个方案可以使领取一份奖品的可能性更大?请用列表法或画树状图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,在与墙平行的一边,开一扇2米宽的门.如果竹篱笆的长为33米,求这个长方形养鸡场与墙垂直的边长是多少?与墙平行的边长是多少?(列方程解答)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=8,AD=10,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com