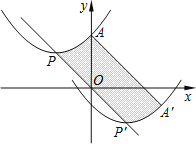
【题目】如图，抛物线的顶点为
，与y轴交于点
若平移该抛物线使其顶点P沿直线移动到点
，点A的对应点为
，则抛物线上PA段扫过的区域
阴影部分
的面积为______．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】完成下面的证明．
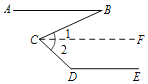
已知：如图，AB∥DE，求证：∠D+∠BCD﹣∠B＝180°．
证明：过点C作CF∥AB．
∵CF∥AB（已作），
∴∠1＝ ．
∵∠2＝∠BCD﹣∠1，
∴∠2＝∠BCD﹣∠B ．
∵AB∥DE，CF∥AB（已知），
∴CF∥DE
∴∠D+∠2＝180°
∴∠D+∠BCD﹣∠B＝180° ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，A(a，0)，B(0，b)，C（-a，0），且
+b2-4b+4=0．
(1)求证：∠ABC=90°；
(2)∠ABO的平分线交x轴于点D，求D点的坐标．
(3)如图，在线段AB上有两动点M、N满足∠MON=45°，求证：BM2+AN2=MN2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高3米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有27米的距离（B，F，C在一条直线上）．
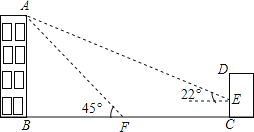
（1）求办公楼AB的高度；
（2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．
（参考数据：sin22°≈
，cos22°≈
，tan22°≈
）
查看答案和解析>>
科目：初中数学 来源： 题型：
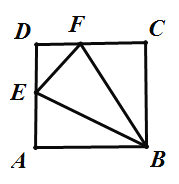
【题目】如图，已知长方形ABCD，点E在线段AD上，将
沿直线BE翻折后，点A落在线段CD上的点F.如果
的周长为12，
的周长为24，那么FC长为________.
查看答案和解析>>
科目：初中数学 来源： 题型：
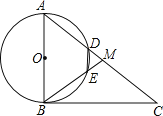
【题目】如图，在
中，
，点M是AC的中点，以AB为直径作
分别交
于点
．
求证：
；
填空：
若
，当
时，
______；
连接
，当
的度数为______时，四边形ODME是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】高斯上小学时，有一次数学老师让同学们计算“从1到100这100个正整数的和”．许多同学都采用了依次累加的计算方法，计算起来非常繁琐，且易出错．聪明的小高斯经过探索后，给出了下面漂亮的解答过程．
解：设S＝1+2+3+…+100 ①
则S＝100+99+98+…+1 ②
①+②，得（即左右两边分别相加）：
2S＝（1+100）+（2+99）+（3+98）+…+（100+1），
＝
，
＝100×101，
所以，S＝
③，
所以，1+2+3+…+100＝5050．
后来人们将小高斯的这种解答方法概括为“倒序相加法”．请你利用“倒序相加法”解答下面的问题．
（1）计算：1+2+3+…+101；
（2）请你观察上面解答过程中的③式及你运算过程中出现的类似③式，猜想：1+2+3+…+n＝ ；
（3）至少用两种方法计算：1001+1002+…+2000．
方法1：
方法2：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，函数y=
的图象与双曲线y=
(k≠0，x>0)相交于点A(3，m)和点B．
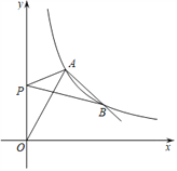
（1）求双曲线的解析式及点B的坐标；
（2）若点P在y轴上，连接PA，PB，求当PA+PB的值最小时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，直线l1：
与坐标轴交于A，B两点，直线l2：
（
≠0）与坐标轴交于点C，D.
（1）求点A，B的坐标；
（2）如图，当=2时，直线l1，l2与相交于点E，求两条直线与
轴围成的△BDE的面积；
（3）若直线l1，l2与轴不能围成三角形，点P（a，b）在直线l2：（k≠0）上，且点P在第一象限.
①求的值；
②若
,，求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
