

| 三角形个数 | 1 | 2 | 3 | 4 |
| 火柴棒根数 | 3 | 5 | 7 | 9 |
分析 (1)观察图形得到第①号图中的火柴棒根数为3根;第②号图中的火柴棒根数为(3+2)根;第③号图中的火柴棒根数为(3+2×2)根;…;
(2)由此可推出第n号图中的火柴棒根数=3+2×(n-1)=(2n+1)根;
(3)由(2)得到2n+1=2011,然后解方程即可.
解答 解:(1)结合图形,发现:后边每多一个三角形,则需要多2根火柴.
搭1个这样的三角形要用3+2×0=3根火柴棒;
搭2个这样的三角形要用3+213=5根火柴棒;
搭3个这样的三角形要用3+2×2=7根火柴棒;
则搭4个这样的三角形要用3+2×3=9根火柴棒;
(2)根据(1)中的规律,得
搭n个这样的三角形要用3+2(n-1)=2n+1根火柴棒.
(3)2n+1=2015,
n=1007,
照这样2015根火柴棒可以摆1007个三角形.
故答案为5,7,9;
点评 此题考查了图形的变化规律,能够结合图形发现规律,即在第一个3根的基础上,后边每多一个三角形,则需要多2根火柴.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
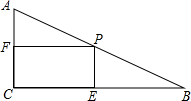 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,动点P从点B开始沿边BA以2cm/s的速度向点A移动,过点P作PE⊥BC,PF⊥AC,设点P移动的时间为t,四边形PECF的面积为S.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,动点P从点B开始沿边BA以2cm/s的速度向点A移动,过点P作PE⊥BC,PF⊥AC,设点P移动的时间为t,四边形PECF的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com