
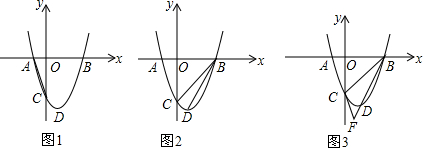
ЗжЮі ЃЈ1ЃЉгЩЬѕМўЧѓЕУЕуAКЭЕуCЕФзјБъЃЌдйАбЫќУЧДњШыХзЮяЯпЕФЗНГЬЧѓГіbЁЂcЕФжЕЃЌПЩЕУХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌзїPNЦНЗжЁЯOPCНЛOCгкЕуNЃЌNMЁЭPCгкMЃЌгЩЁїPONЁзЁїBCDЃЌЕУ$\frac{OP}{BC}$=$\frac{ON}{DC}$ЃЌМД$\frac{ON}{OP}$=$\frac{DC}{BC}$=$\frac{1}{3}$ЃЌЩшON=aЃЌдђOP=3aЃЌдкRtMNCжаРћгУЙДЙЩЖЈРэМДПЩЧѓГіaНтОіЮЪЬтЃЎ
ЃЈ3ЃЉзїPHЁЭACЕФбгГЄЯпгыЕуHЃЌзїAMЁЭPQгкЕуMЃЌИљОнжБНЧШ§НЧаЮЕФаджЪЧѓГіЁЯHPA=ЁЯOCAЃЎЩшHA=aЃЌдђPH=3aЃЌгЩЕШбќжБНЧШ§НЧаЮЕФаджЪгУaБэЪОГіHFЃЌAFМАPFЕФГЄЃЌИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхЕУГіcosЁЯAFPЕФжЕЃЌзїQSЁЭxжсгкЕуSЃЌЩшQЃЈtЃЌt2-2t-3ЃЉЃЌдђQS=-t2+2t+3=-ЃЈt+1ЃЉЃЈt-3ЃЉЃЌPS=4+tЃЌдйгЩtanЁЯSPQ=$\frac{QS}{PS}$=$\frac{1}{2}$ЃЌЧѓГіtЕФжЕЃЌгЩДЫПЩЕУГіНсТлЃЎ
НтД№ 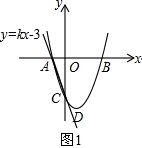 НтЃКЃЈ1ЃЉШчЭМ1ЃЌЁпжБЯпACЕФНтЮіЪНЮЊy=kx-3ЃЌ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЁпжБЯпACЕФНтЮіЪНЮЊy=kx-3ЃЌ
Сюx=0ЃЌЕУy=-3ЃЌ
ЁрCЃЈ0ЃЌ-3ЃЉЃЎ
гжЁпtanЁЯACO=$\frac{1}{3}$ЃЌ
ЁрAЃЈ-1ЃЌ0ЃЉЃЎ
Ёр$\left\{\begin{array}{l}c=-3\\ЃЈ-1ЃЉ^{2}+bЁСЃЈ-1ЃЉ+c=0\end{array}\right.$ЃЌ
НтЕУb=-2ЃЌc=-3ЃЌ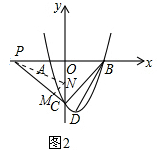
ЁрХзЮяЯпy=x2-2x-3ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌзїPNЦНЗжЁЯOPCНЛOCгкЕуNЃЌNMЁЭPCгкMЃЌ
ЁпBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ-3ЃЉЃЌDЃЈ1ЃЌ-4ЃЉЃЌ
ЁрOB=OCЃЌBC=3$\sqrt{2}$ЃЌCD=$\sqrt{2}$ЃЌBD=2$\sqrt{5}$ЃЌ
ЁрDC2+BC2=BD2ЃЌ
ЁрЁЯDCB=90ЁуЃЌ
ЁпЁЯOPC=2ЁЯCBDЃЌ
ЁрЁЯOPN=ЁЯCBDЃЌЁЯPON=ЁЯBCD=90ЁуЃЌ
ЁрЁїPONЁзЁїBCDЃЌ
Ёр$\frac{OP}{BC}$=$\frac{ON}{DC}$ЃЌМД$\frac{ON}{OP}$=$\frac{DC}{BC}$=$\frac{1}{3}$ЃЌЩшON=aЃЌдђOP=3aЃЌ
ЁпЁЯNPO=ЁЯNPMЃЌNOЁЭPOЃЌNMЁЭPMЃЌ
ЁрON=MN=aЃЌNC=3-aЃЌ
ЁпЁЯMCN=ЁЯPCOЃЌЁЯNMC=ЁЯPOC=90ЁуЃЌ
ЁрЁїCMNЁзЁїCOPЃЌ
Ёр$\frac{CM}{OC}$=$\frac{MN}{OP}$ЃЌ
ЁрCM=1ЃЌ
дкRtЁїCMNжаЃЌЁпCM2+MN2=CN2ЃЌ
Ёр1+a2=ЃЈ3-aЃЉ2ЃЌ
Ёрa=$\frac{4}{3}$ЃЌ
ЁрOP=3a=4ЃЌ
ЁрЕуPЕФзјБъЮЊPЃЈ-4ЃЌ0ЃЉЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌзїPHЁЭACЕФбгГЄЯпгыЕуHЃЌзїAMЁЭPQгкЕуMЃЌдђЁЯPHF=90ЁуЃЎ
ЁпЁЯAOC=90ЁуЃЌ
ЁрЁЯPHF=ЁЯAOC=90ЁуЃЎ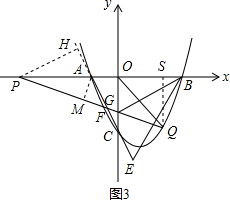
ЁпЁЯPAH=ЁЯCAOЃЌ
Ёп180Ёу-ЁЯPHF-ЁЯPAH=180Ёу-ЁЯAOC-ЁЯCAOЃЌ
ЁрЁЯHPA=ЁЯOCAЃЎ
ЁпtanЁЯACO=$\frac{1}{3}$ЃЌ
ЁрtanЁЯHPA=$\frac{HA}{PH}$=$\frac{1}{3}$ЃЎ
ЩшHA=aЃЌдђPH=3aЃЌ
ЁпЁЯHFA=45ЁуЃЌ
ЁрЁЯHPF=90Ёу-ЁЯPFH=45ЁуЃЌ
ЁрЁЯPFA=ЁЯHPFЃЌ
ЁрPH=HFЃЌ
ЁрHF=3aЃЌ
ЁрAF=HF-HA=3a-a=2aЃЌ
ЁрPF=3$\sqrt{2}$aЃЎ
ЁрcosЁЯAFP=$\frac{MF}{AF}$=$\frac{\sqrt{2}}{2}$ЃЌ
ЁрMF=$\frac{\sqrt{2}}{2}$AF=$\sqrt{2}$aЃЌ
ЁрAM=$\sqrt{2}$aЃЎ
ЁрtanЁЯBPQ=$\frac{MA}{PA}$=$\frac{\sqrt{2}a}{2\sqrt{2}a}$=$\frac{1}{2}$ЃЎ
зїQSЁЭxжсгкЕуSЃЌЩшQЃЈtЃЌt2-2t-3ЃЉЃЌдђQS=-t2+2t+3=-ЃЈt+1ЃЉЃЈt-3ЃЉЃЌPS=4+tЃЌ
дкRtЁїPSQжаЃЌЁпtanЁЯSPQ=$\frac{QS}{PS}$=$\frac{1}{2}$ЃЌ
Ёр4+t=-2ЃЈt+1ЃЉЃЈt-3ЃЉЃЌНтЕУt1=2ЃЌt2=-$\frac{1}{2}$ЃЈЩсШЅЃЉЃЌ
ЁрQЃЈ2ЃЌ-3ЃЉЃЎ
ДЫЪБBG=OQЃЌBGЁЭOQЃЎ
ЕуЦР БОЬтПМВщСЫЖўДЮКЏЪ§злКЯЬтЃЌЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЁЂНЧЦНЗжЯпЕФаджЪЖЈРэЁЂШёНЧШ§НЧКЏЪ§ЁЂЙДЙЩЖЈРэЕШжЊЪЖЃЌНтЬтЕФЙиМќЪЧбЇЛсЬѕМўГЃгУИЈжњЯпЃЌбЇЛсРћгУВЮЪ§ЃЌЙЙНЈЗНГЬЕФЫМЯыНтОіЮЪЬтЃЌЬхЯжСЫзЊЛЏЁЂЪ§аЮНсКЯЕФЪ§бЇЫМЯыЃЌФбЖШНЯДѓЃЌЪєгкжаПМбЙжсЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
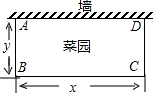 РюДѓвЏвЊЮЇГЩвЛИіОиаЮВЫдАЃЌВЫдАЕФвЛБпРћгУзуЙЛГЄЕФЧНЁЂгУРщАЪЮЇГЩЕФСэЭтШ§БпзмГЄЧЁКУЮЊ24УзЃЌвЊЮЇГЩЕФВЫдАЪЧШчЭМЫљЪОЕФГЄЗНаЮABCDЃЌЩшBCБпЕФГЄЮЊxУзЃЌABБпЕФГЄЮЊyУзЃЎ
РюДѓвЏвЊЮЇГЩвЛИіОиаЮВЫдАЃЌВЫдАЕФвЛБпРћгУзуЙЛГЄЕФЧНЁЂгУРщАЪЮЇГЩЕФСэЭтШ§БпзмГЄЧЁКУЮЊ24УзЃЌвЊЮЇГЩЕФВЫдАЪЧШчЭМЫљЪОЕФГЄЗНаЮABCDЃЌЩшBCБпЕФГЄЮЊxУзЃЌABБпЕФГЄЮЊyУзЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ОиаЮ | BЃЎ | СтаЮ | CЃЎ | е§ЗНаЮ | DЃЎ | ЦНааЫФБпаЮ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com