
����Ŀ��ij��˾Ӫ��![]() ���ֲ�Ʒ�������г����У�ȷ��������Ϣ��
���ֲ�Ʒ�������г����У�ȷ��������Ϣ��
��Ϣ1������![]() �ֲ�Ʒ��������
�ֲ�Ʒ��������![]() (��Ԫ)�������۲�Ʒ
(��Ԫ)�������۲�Ʒ![]() (��)֮����ڶ��κ�����ϵ����ͼ��ʾ
(��)֮����ڶ��κ�����ϵ����ͼ��ʾ
��Ϣ2������![]() �ֲ�Ʒ��������
�ֲ�Ʒ��������![]() (��Ԫ)�����۲�Ʒ
(��Ԫ)�����۲�Ʒ![]() (��)֮�����������������ϵ
(��)֮�����������������ϵ![]()
����������Ϣ������������⣺
��1������κ����ı���ʽ��
��2���ù�˾������![]() ���ֲ�Ʒ��10�֣������һ��Ӫ������ʹ����
���ֲ�Ʒ��10�֣������һ��Ӫ������ʹ����![]() ���ֲ�Ʒ��õ�����֮�������������Ƕ�����Ԫ?
���ֲ�Ʒ��õ�����֮�������������Ƕ�����Ԫ?
���𰸡���1��![]() ����2������A��Ʒ6�֣�����B��Ʒ4�֣�����֮��������Ϊ6.6��Ԫ
����2������A��Ʒ6�֣�����B��Ʒ4�֣�����֮��������Ϊ6.6��Ԫ
��������
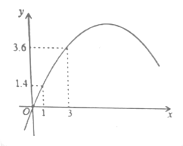
(1)�������߹�ԭ�����y��x��ĺ�����ϵʽΪy=ax2+bx+c�������ô���ϵ�������ɵã�
(2)�蹺��A��Ʒm�֣�����B��Ʒ(10m)�֣�����A��B���ֲ�Ʒ��õ�����֮��ΪWԪ�����ݣ�A��Ʒ����+B��Ʒ����=������ɵ�W=0.1m2+1.5m+0.3(10m)���䷽����ݶ��κ��������ʼ���֪��ֵ�����
�⣺(1)����κ����ı���ʽΪy=ax2+bx+c��
��ͼ�������߹���(0,0)��(1,1.4)��(3,3.6)��
�����������������ʽ��
��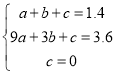 ,
,
���
���Զ��κ����ı���ʽΪy=0.1x2+1.5x��
(2)�蹺��A��Ʒm�֣�����B��Ʒ(10m)�֣�����A��B���ֲ�Ʒ��õ�����֮��ΪWԪ��
��W=0.1m2+1.5m+0.3(10m)��
=0.1m2+1.2m+3��
=0.1(m6)2+6.6��
��0.1<0��
��൱m=6ʱ��Wȡ�����ֵ�����ֵΪ6.6��Ԫ��
�𣺹���A��Ʒ6�֣�����B��Ʒ4�֣�����A��B���ֲ�Ʒ��õ�����֮��������������6.6��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�п�ѧ�����ذ��̳���һ�ι���A��B����Ʒ�Ƶ�������AƷ��������3200Ԫ������BƷ��������2400Ԫ���ҹ���AƷ�����������ǹ���BƷ������������2������֪����һ��BƷ������ȹ���һ��AƷ�Ƶ�����20Ԫ��
��1������һ��AƷ�ơ�һ��BƷ�Ƶ�����������Ԫ��
��2������һ��Ϊ�ٰ������������������ڶ��ι���A��B����Ʒ������ǡ���ذ��̳�������Ʒ��������ۼ۽��е�����AƷ�������ۼ۱ȵ�һ�ι���ʱ�����aԪ��a��0����BƷ������һ�ι���ʱ�ۼ۵�9�۳��ۣ�����ڶ��ι���AƷ������ĸ����ȵ�һ����2a�����ڶ��ι���BƷ������ĸ����ȵ�һ�ζ�![]() ������ڶ��ι���A��B����Ʒ��������ܷ��ñȵ�һ����320Ԫ����a��ֵ��
������ڶ��ι���A��B����Ʒ��������ܷ��ñȵ�һ����320Ԫ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�������˸��ţ����ǣ��������£�ij��ѧΪ����ѧ����Ұ����չ������ѧ��ѧ�������������˾��꼶����ѧ��һ�ܵĿ���ѧϰ��ѧʱ�䣬����������Ƴ�������������ͳ��ͼ���������ͳ��ͼ����Ϣ�ش��������⣺
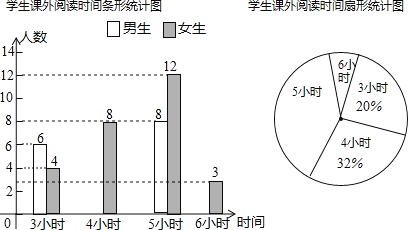
��1�����ε����ѧ������Ϊ____________�ˣ�������ѧ������ѧϰ��ѧʱ�����λ����____________Сʱ��������������������Сʱ��
��2�����㲹ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�����ѧϰ��ѧʱ��Ϊ5Сʱ�����ε�Բ�ĽǶ�����____________��
��4�����꼶��ѧ��700�ˣ����ƾ��꼶һ�ܿ���ѧϰ��ѧʱ�䲻����5СʱСʱ��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����MNΪֱ�����뾶Ϊ4��Բ��PΪ��MΪԲ�ġ�2Ϊ�뾶��Բ��һ�㣬����P����M�����߽���O�ڵ�A��B����MA,MB,��MA��MBΪ_____��
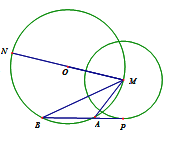
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮƽ��������һ��Բ��ˮ�أ�ֱ��AB��Ϊ6m����Ϊ![]() m��һ���AC��ֱ�ڵ��棨AC�����������ֱ�߶���ֱ����
m��һ���AC��ֱ�ڵ��棨AC�����������ֱ�߶���ֱ����
��1����PΪ��AB���е㣬��˵����BPC=90��
��2����P��ABΪ������һ�㣨����A��B�غϣ�����BPC=90�㻹������Ϊʲô��
��3����AB���Ƿ���ڵ�Pʹ��PAB����PAC���ƣ���������![]() ��ֵ�������ڣ�˵�����ɣ�
��ֵ�������ڣ�˵�����ɣ�
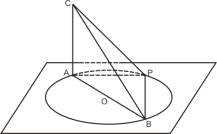
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��y��kx+1��x�ᡢy��ֱ��ཻ�ڵ�A��B������AOB�Ƶ�A˳ʱ����ת��ʹAO����AB�ϣ��õ���ACD������ACD������BAƽ�ƣ�����D����x��ʱ�˶�ֹͣ����ƽ�ƾ���Ϊm��ƽ�ƺ��ͼ����x���·����ֵ����ΪS��S����m�ĺ���ͼ����ͼ2��ʾ������0��m��2��2��m��aʱ�������Ľ���ʽ��ͬ��
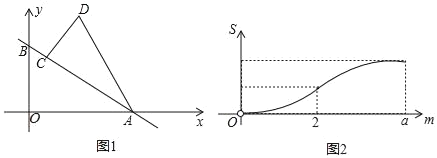
��1����գ�a���� ����k���� ����
��2����S����m�Ľ���ʽ����д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У���P�ӵ�D����������D��A���������˶��������A��ֹͣ�˶�����Q�ӵ�D����������D��C��B��A�ķ��������˶��������A��ֹͣ�˶��� ��֪��P���˶��ٶ�Ϊ4��ͼ�ڱ�ʾP��Q����ͬʱ����x�����APQ�����Ϊy��x�ĺ�����ϵ�����Q���˶��ٶȿ����ǣ� ��
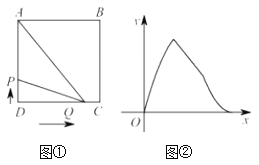
A.2B.3C.8D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y����x2+bx+c������A��B��C����֪A����1��0����C��0��3����
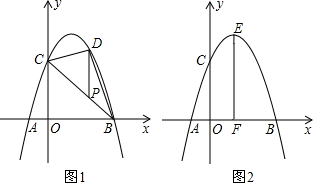
��1���������ߵĽ���ʽ��
��2����ͼ1��PΪ�߶�BC��һ���㣬����P��y���ƽ���ߣ����������ڵ�D���Ƿ����������P�㣬ʹ�߶�PD�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3����ͼ2�������ߵĶ���ΪE��EF��x���ڵ�F��N��ֱ��EF��һ���㣬M��m��0����x��һ�����㣬��ֱ��д��CN+MN+![]() MB����Сֵ�Լ���ʱ��M��N�����ֱ꣬��д���������˵�����ɣ�
MB����Сֵ�Լ���ʱ��M��N�����ֱ꣬��д���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
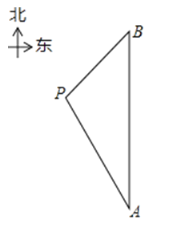
����Ŀ����һ�κ��Ͼ�Ԯ�У�����רҵ������![]() ͬʱ�յ�ij�¹��洬�����ѶϢ����֪��ʱ������
ͬʱ�յ�ij�¹��洬�����ѶϢ����֪��ʱ������![]() ��
��![]() �����������¹��洬
�����������¹��洬![]() �ھ�����
�ھ�����![]() �ı�ƫ��30�������ϣ��ھ�����
�ı�ƫ��30�������ϣ��ھ�����![]() �����Ϸ����ϣ����¹��洬
�����Ϸ����ϣ����¹��洬![]() �������
�������![]() ���120���
���120���
��1�����յ����ѶϢʱ�¹��洬![]() �������
�������![]() ֮��ľ��룻
֮��ľ��룻
��2����������A��![]() �ֱ���40����/Сʱ��30����/Сʱ���ٶ�ͬʱ����������ֱ��ǰ���¹��洬
�ֱ���40����/Сʱ��30����/Сʱ���ٶ�ͬʱ����������ֱ��ǰ���¹��洬![]() ���Ѿȣ���ͨ�������ж����Ҵ��ȵ��
���Ѿȣ���ͨ�������ж����Ҵ��ȵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com