
【题目】如图,已知 DE∥ BC, AE=50cm, EC=30cm, BC=70cm,∠ BAC=45°,∠ ACB=40°.
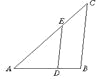
求(1)∠ AED和∠ ADE的度数;(2) DE的长.
【答案】(1)∠ AED=40°,∠ ADE=95°;(2) DE= ![]() cm.
cm.
【解析】试题分析:
(1)在△ABC中,由∠ BAC=45°,∠ ACB=40°易得∠B=95°,结合DE∥BC可得∠AED=∠ACB=40°,∠ADE=∠B=95°;
(2)由AE=50cm,EC=30cm可得AC=80cm;由DE∥BC可得△ADE∽△ABC,结合BC=70cm即可由相似三角形对应边成比例即可求得DE的长.
试题解析:
(1)∵在△ABC中,∠ BAC=45°,∠ ACB=40°,
∴∠B=180°-45°-40°=95°,
∵DE∥BC,
∴∠AED=∠ACB=40°,∠ADE=∠B=95°;
(2)∵AE=50cm,EC=30cm,
∴AC=80cm.
∵DE∥BC,
∴△ADE∽△ABC,
∴![]() ,
,
又∵BC=70cm,
∴DE=![]() cm.
cm.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞士的一位中学教师巴尔末从光谱数据![]() ,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点的坐标分别为A![]() ,B(2,0),直线AB与反比例函数
,B(2,0),直线AB与反比例函数![]() 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
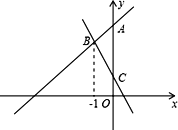
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.
①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于 ;
(2)直线y=kx+4(k≠0)与x轴交于点E(x 0 ,0),若﹣2<x 0 <﹣1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
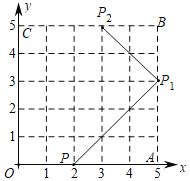
A.(5,3)B.(3,5)C.(0,2)D.(2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种新型节能台灯,已知B型节能台灯每盏进价比A型的多40元,且用3000元购进的A型节能台灯与用5000元购进的B型节能台灯的数量相同.
(1)求每盏A型节能台灯的进价是多少元?
(2)商场将购进A、B两型节能台灯100盏进行销售,A型节能台灯每盏的售价为90元,B型节能台灯每盏的售价为140元,且B型节能台灯的进货数量不超过A型节能台灯数量的2倍.应怎样进货才能使商场在销售完这批台灯时利最多?此时利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前小明花1200元从市场购进批发价分别为每箱30元与50元的![]() 、
、![]() 两种水果进行销售,分别以每箱35元与60元的价格出售,设购进
两种水果进行销售,分别以每箱35元与60元的价格出售,设购进![]() 水果
水果![]() 箱,
箱,![]() 水果
水果![]() 箱.
箱.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)若要求购进![]() 水果的数量不少于
水果的数量不少于![]() 水果的数量,则应该如何分配购进
水果的数量,则应该如何分配购进![]() 、
、![]() 水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且甲种数量不超过乙种的2倍,则如何购买总费用最低?最低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com